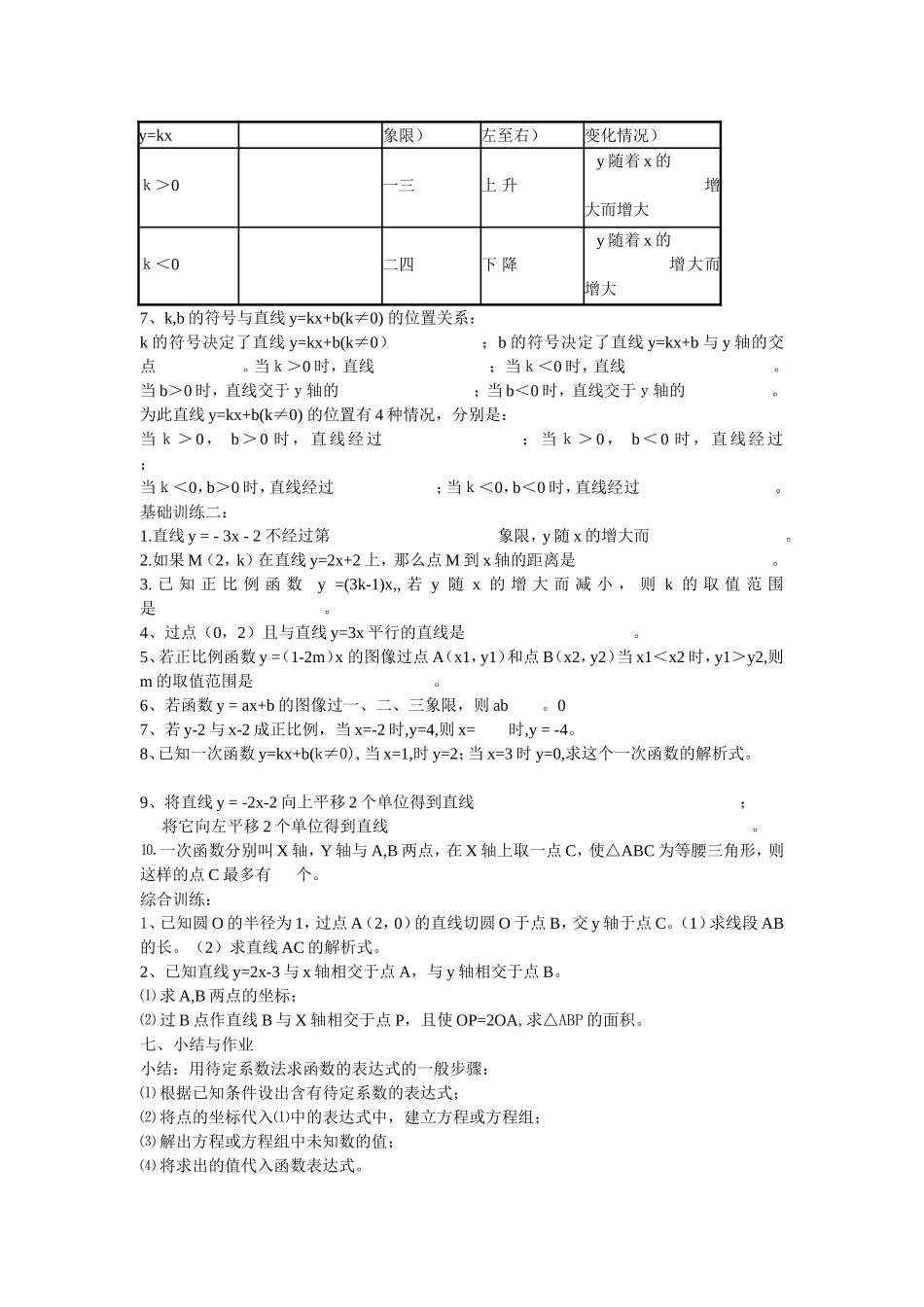
初三一次函数复习(一)孙力君一、教学目标:1、知道一次函数与正比例函数的定义;2、理解掌握一次函数的图象的特征和相关的性质;体会数形结合思想;3、弄清一次函数与正比例函数的区别与联系;4、熟练运用待定系数法求一次函数的解析式。二、教学重、难点:重点:初步构建比较系统的函数知识体系,能应用本章的基础知识熟练地解决数学问题。难点:运用一次函数的图像和性质解决含字母参数的问题,体会数形结合与方程思想。三、教学准备:课件、电脑、投影仪四、教学方法:例证法、探究法五、教学设计简介:因为这是初三总复习节段的复习课,在这之前已经复习了变量、函数的定义、表示法及图象,而本节的教学任务是一次函数的基础知识及其简单的应用,没有涉及实际应用。为了节约学生的时间,打造高效课堂,我开门见山,直接向学生展示教学目标,然后让学生根据本节课的复习目标进行联想回顾,变被动学习为主动学习。例如,在“图象及其性质”环节中,老师让学生自己说出一次函数图象的形状、位置及增减性,不完整的可让其他学生补充纠正。这样,使无味的复习课变得活跃一些,增强学习气氛。随后教师就用大屏幕展示出标准答案,然后教师组织学生以比赛的形式做一些针对性的练习。六、教学过程:1、一次函数与正比例函数的定义:一次函数:一般地,若y=kx+b(其中k,b为常数且k≠0),那么y是x的一次函数正比例函数:对于y=kx+b,当b=0,k≠0时,有y=kx,此时称y是x的正比例函数,k为正比例系数。2.一次函数与正比例函数的区别与联系:(1)从解析式看:y=kx+b(k≠0,b是常数)是一次函数;而y=kx(k≠0,b=0)是正比例函数,显然正比例函数是一次函数的特例,一次函数是正比例函数的推广。(2)从图象看:正比例函数y=kx(k≠0)的图象是过原点(0,0)的一条直线;而一次函数y=kx+b(k≠0)的图象是过点(0,b)且与y=kx平行的一条直线。基础训练一:1、指出下列函数中的正比例函数和一次函数:①y=x+1;②y=-x/5;③y=3/x;④y=4x;⑤y=x(3x+1)-3x;⑥y=3(x-2);⑦y=x/5-1/2。2、下列给出的两个变量中,成正比例函数关系的是:A、少年儿童的身高和年龄;B、长方形的面积一定,它的长与宽;C、圆的面积和它的半径;D、匀速运动中速度固定时,路程与时间的关系。3、对于函数y=(k+1)x+2-b,当k、b满足什么条件时为正比例函数?当k满足什么条件时为一次函数?3、正比例函数、一次函数的图象和性质:正比例函数图象位置(经过的变化趋势(从增减性(y随着x的y=kx象限)左至右)变化情况)k>0一三上升y随着x的增大而增大k<0二四下降y随着x的增大而增大7、k,b的符号与直线y=kx+b(k≠0)的位置关系:k的符号决定了直线y=kx+b(k≠0);b的符号决定了直线y=kx+b与y轴的交点。当k>0时,直线;当k<0时,直线。当b>0时,直线交于y轴的;当b<0时,直线交于y轴的。为此直线y=kx+b(k≠0)的位置有4种情况,分别是:当k>0,b>0时,直线经过;当k>0,b<0时,直线经过;当k<0,b>0时,直线经过;当k<0,b<0时,直线经过。基础训练二:1.直线y=-3x-2不经过第象限,y随x的增大而。2.如果M(2,k)在直线y=2x+2上,那么点M到x轴的距离是。3.已知正比例函数y=(3k-1)x,,若y随x的增大而减小,则k的取值范围是。4、过点(0,2)且与直线y=3x平行的直线是。5、若正比例函数y=(1-2m)x的图像过点A(x1,y1)和点B(x2,y2)当x1<x2时,y1>y2,则m的取值范围是。6、若函数y=ax+b的图像过一、二、三象限,则ab。07、若y-2与x-2成正比例,当x=-2时,y=4,则x=时,y=-4。8、已知一次函数y=kx+b(k≠0),当x=1,时y=2;当x=3时y=0,求这个一次函数的解析式。9、将直线y=-2x-2向上平移2个单位得到直线;将它向左平移2个单位得到直线。⒑一次函数分别叫X轴,Y轴与A,B两点,在X轴上取一点C,使△ABC为等腰三角形,则这样的点C最多有个。综合训练:1、已知圆O的半径为1,过点A(2,0)的直线切圆O于点B,交y轴于点C。(1)求线段AB的长。(2)求直线AC的解析式。2、已知直线y=2x-3与x轴相交于点A,与y轴相交于点B。⑴求A,B两点的坐标;⑵过B点作直线B与X轴相交于点P,且使OP=2OA,求△ABP的面积。七、小结...