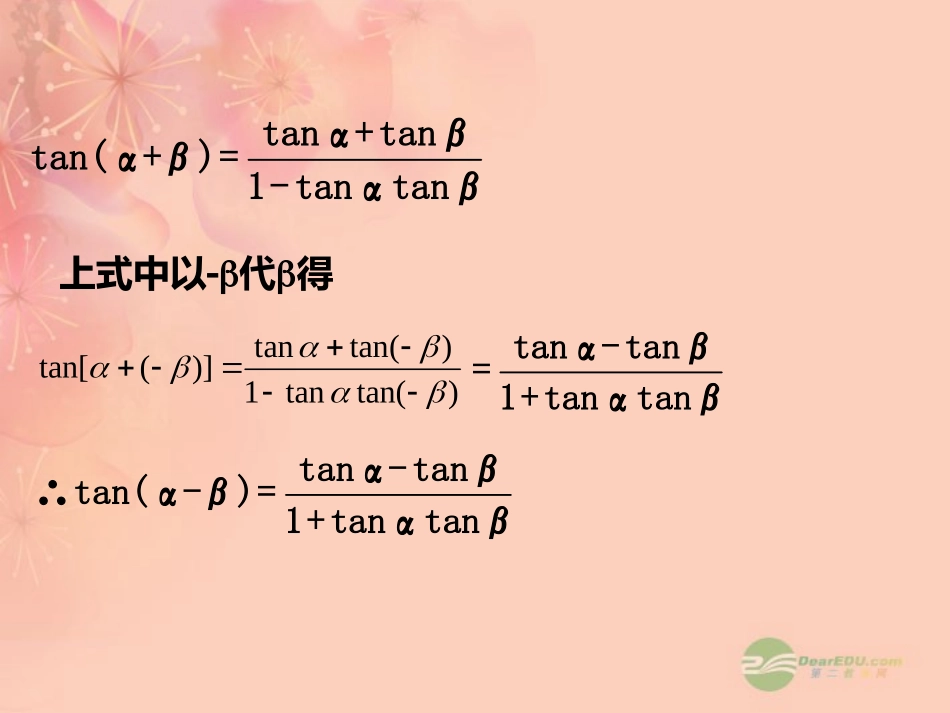高一数学 312两角和与差的正切课件VIP免费

3.1两角和与差的三角公式(2)两角和的正切公式：sinαcosβ+cosαsinβcosαcosβ-sinαsinβsin(α+β)cos(α+β)coscos0当时，coscos分子分母同时除以tanα+tanβtan(α+β)=1-tanαtanβtan()上式中以代得tanα+tanβtan(α+β)=1-tanαtanβtantan()tan[()]1tantan()tanα-tanβ=1+tanαtanβtanα-tanβ∴tan(α-β)=1+tanαtanβtanαtanβtan(αβ)=1tan++-αtanβtanαtanβtan(αβ)=1tan--+αtanβ注意：1必须在定义域范围内使用上述公式。2注意公式的结构，尤其是符号。即：tan，tan，tan(±)只要有一个不存在就不能使用这个公式，只能（也只需）用诱导公式来解。如:已知tan=2,求不能用tan()2两角和与差的正切公式问:如何求cot(a+β)?有关两角和差的余切问题，一般都是将它由同角公式的倒数关系化为两角和差的正切，用公式来解决．11+tanαtanβcot(α-β)==tan(α-β)tanα-tanβ11-tanαtanβcot(α+β)==tan(α+β)tanα+tanβ33sin,sin(),54cos(),tan()44a例：已知是第四象限的角，求的值。,3解：由sin=-是第四象限的角，得522354cos1sin1(),5sin3tancos4所以)sincoscossin444于是有sin(242372();252510)coscossinsin444cos(242372();252510tantantan14tan()41tan1tantan4314731()44cos4cossin4;(2)cos20cos70sin20sin70;1tan15(3).tan15。。。。。。。。。。例：利用和（差）角公式计算下列各式的值：（1)sin7227221-cos4cossin41sin(4)sin30;2。。。。。。。解：（1)由公式得：sin722722722(2)cos20cos70sin20sin70cos(2070)cos900。。。。。。。1tan15tan45tan15(3)tan15tan45tan15tan(4515)tan603。。。。。。。。。1-1-1:求tan15和tan75的值：解：tan15=tan(4530)=32636123333331331ooootan45-tan301+tan45tan30tan75=tan(45+30)=313312633633313=2+32、化简：(1)tan(α+β)(1-tanαtanβ)tan(α-β)+tanβ(2)1-tan(α-β)tanβ3、求值：ooootan71-tan26(1)1+tan71tan26oo1-3tan75(2)3+tan75答案:(1)tanα+tanβ(2)tanα答案:(1)1(2)-1tanα+tanβtan(α+β)=1-tanαtanβtanα-tanβtan(α-β)=1+tanαtanβ变形：tanα+tanβ=tan(α+β)(1-tanαtanβ)tanα-tanβ=tan(α-β)(1+tanαtanβ)tantan(1tanαtanβ)=tan()sin)sincoscossin(sin)sincoscossin(求下列各式的值：(1)75tan175tan1(2)tan17+tan28+tan17tan28解：1原式=3120tan)7545tan(75tan45tan175tan45tan2∵28tan17tan128tan17tan)2817tan(∴tan17+tan28=tan(17+28)(1tan17tan28)=1tan17tan28∴原式=1tan17tan28+tan17tan28=131sincos22(1)把下列各式化为一个角的三角函数形式sincos(2)sincosxbx(3)asincosxbxa化为一个角的三角函数形式sincosxbxa222222sincosbabxxababa令2222cossinabbaba22sincoscossinxabx22sinabx22cosabx把下列各式化为一个角的三角函数形式sincos(1)231sincos22(2)sincos44xx26(3)44cos15sin15cos15sin152sin()2sin()3cos().333xxx1、化简：2、化简：4sincos.yxx、(1)求函数的值域3sin233cos21yxxxx(2)函数的最小值是，对应的值是；最大值是，对应的的值是？3、