高中数学 32(立体几何中的向量方法(四))课件 新人教B版选修2-1 课件VIP免费

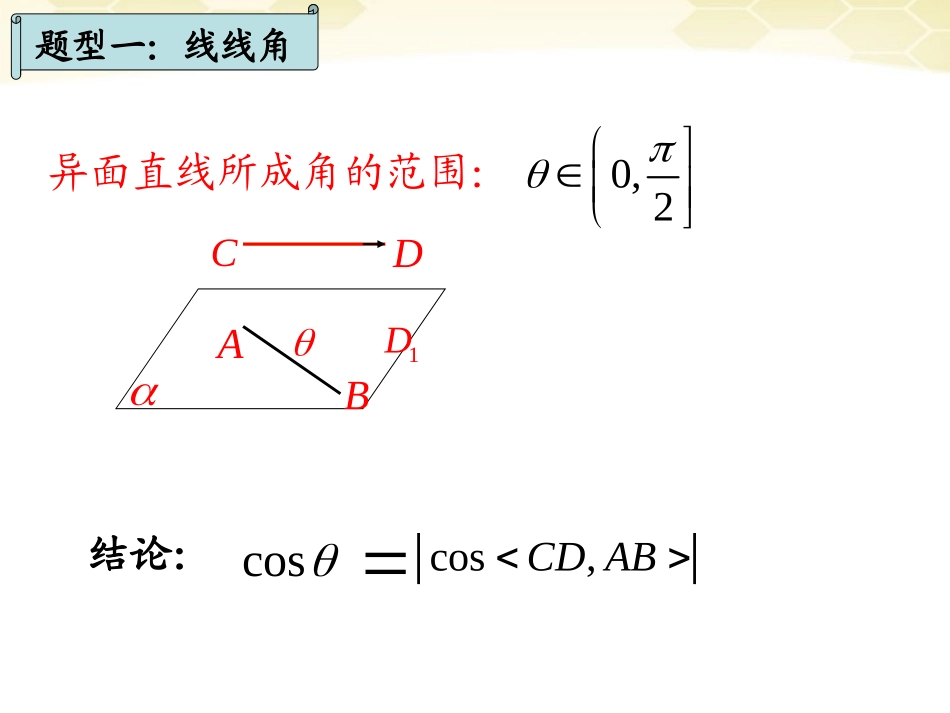
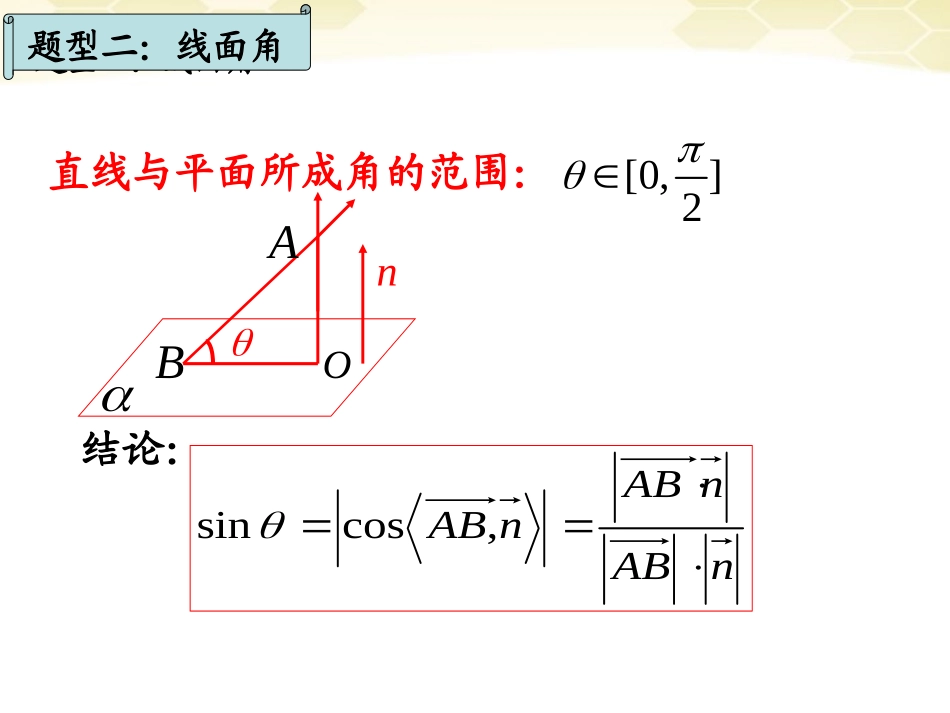
3.2利用向量解决空间角问题异面直线所成角的范围：0,2ABCD1D结论：coscos,CDAB�||题型一：线线角题型二：线面角直线与平面所成角的范围：[0,]2ABOn结论：题型二：线面角nABnABnAB,cossin练习：1111ABCDABCD的棱长为1.111.BCABC求与面所成的角题型二：线面角正方体ABCD1A1B1C1D题型三：二面角二面角的范围：[0,]1n�2n�2n�1n�cos12|cos,|nn�cos12|cos,|nn�ABO关键：观察二面角的范围题型三：二面角,1,1,,2.AABCDSAABBCADSCDSBA0例三如所示，ABCD是一直角梯形，ABC=90S平面求面与面所成二面角的余弦值ABCDS,1,1,,2.AABCDSAABBCADSCDSBA0例三如所示，ABCD是一直角梯形，ABC=90S平面求面与面所成二面角的余弦值ABCDSxyz解：建立空直角坐系A-xyz如所示,A(0,0,0),11(1,,0),(0,,1)22CDSD�C(-1,1,0),1,0),2D(0,(0,0,1)S11(0,,0)2SBAnAD��易知面的法向量设平面2(,,),SCDnxyz�的法向量22,,nCDnSD�由得：0202yxyz22yxyz2(1,2,1)n�任取1212126cos,3||||nnnnnn���63即所求二面角得余弦值是小结：1.异面直线所成角：coscos,CDAB�||2.直线与平面所成角：sincos,nAB��||3.二面角：cos12|cos,|nn�关键：观察二面角的范围ABCD1DABOn1n�2n�cos12|cos,|nn�