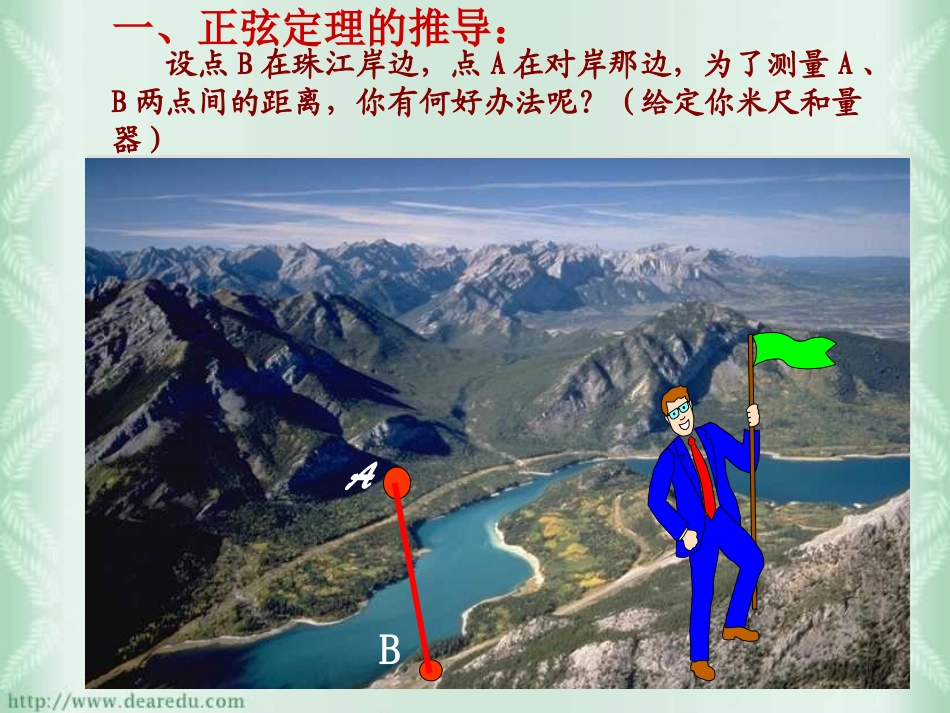
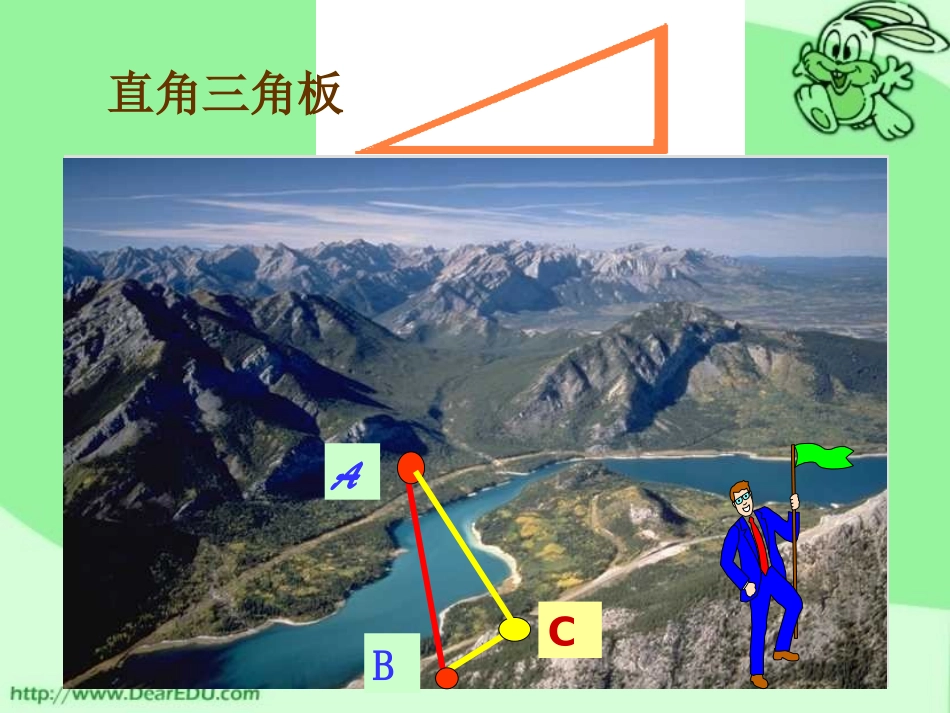
AB设点B在珠江岸边,点A在对岸那边,为了测量A、B两点间的距离,你有何好办法呢?(给定你米尺和量器)一、正弦定理的推导:直角三角板ABCABC设问?若将点C移到如下图所示的位置,你还能求出A、B两点间的距离吗?如图:在RtABC△中,我们能很快发现:提问1:在这里,你能发现一些结论吗?结论:提问2:这个等式对于锐角三角形或者钝角三角形中是否成立呢?引子:结论:AD=提问3:大家在直角三角形中比较容易得到:那么大家能不能也借助于构造直角三角形,来研究锐角三角形中该等式是不是也成立呢?提问4:这个三角形的高线AD能不能起个桥梁作用呢?CcBbsinsin提问5:这个三角形有几条高?是不是也能得到一些等式关系?可得到:sinBbsinAaCcAasinsin同理:钝角三角形也满足等式:很显然,对于锐角三角形而言:等式也是成立的。CcBbAasinsinsin提问6:那么,对于钝角三角形而言,该等式是不是也成立呢?注意:同样是构造直角三角形来解次这一问题。结论:AD=CcBbsinsinCcBbAasinsinsin由以上推论可知:对于作何三角形而言,都有:三角形各边和其所对角的正弦值之比相等,即:CcBbAasinsinsin这就是正弦定理提问7:在正弦定理公式中,你能发现哪些问题?又会不会产生一些相关的变形呢?变形:2.a:b:c=SinA:SinB:SinC3.a=kSinA,b=kSinB,c=kSinC0)k(ksinCcsinBbsinAa1.注:有了正弦定理,前面的设问可就比较容易解决了提问8:正弦定理在解决三角形问题中到底有哪些应用呢?提醒:三角形是由3条边和3个角组成的,那么我们在运用“正弦定理”解三角形时,只需知道其中几个量,就可求出余下的几个量?有没有前提条件?结论:正弦定理的运用条件:1。已知三角形的两角及任一边;2。已知三角形的两边及其一边所对的角。注意:已知三角形的的某些边和角,求其他边和角的过程叫做解三角形。二、典例分析:例1:已知△ABC中,A=450,C=300,c=10,求b.例2:在△ABC中,a=4,b=4,B=450,求A。2sinBsinABA性质:之。外接圆的半径,试证明为,其中以进一步深化为思考题:正弦定理还可ABCRRCcBbAa2sinsinsin?三、练习巩固四、小结与作业小结:主要内容:1。正弦定理;2。正弦定理的运用条件。作业:1。课本P9(1-3)2。研究探讨P11(9-10)