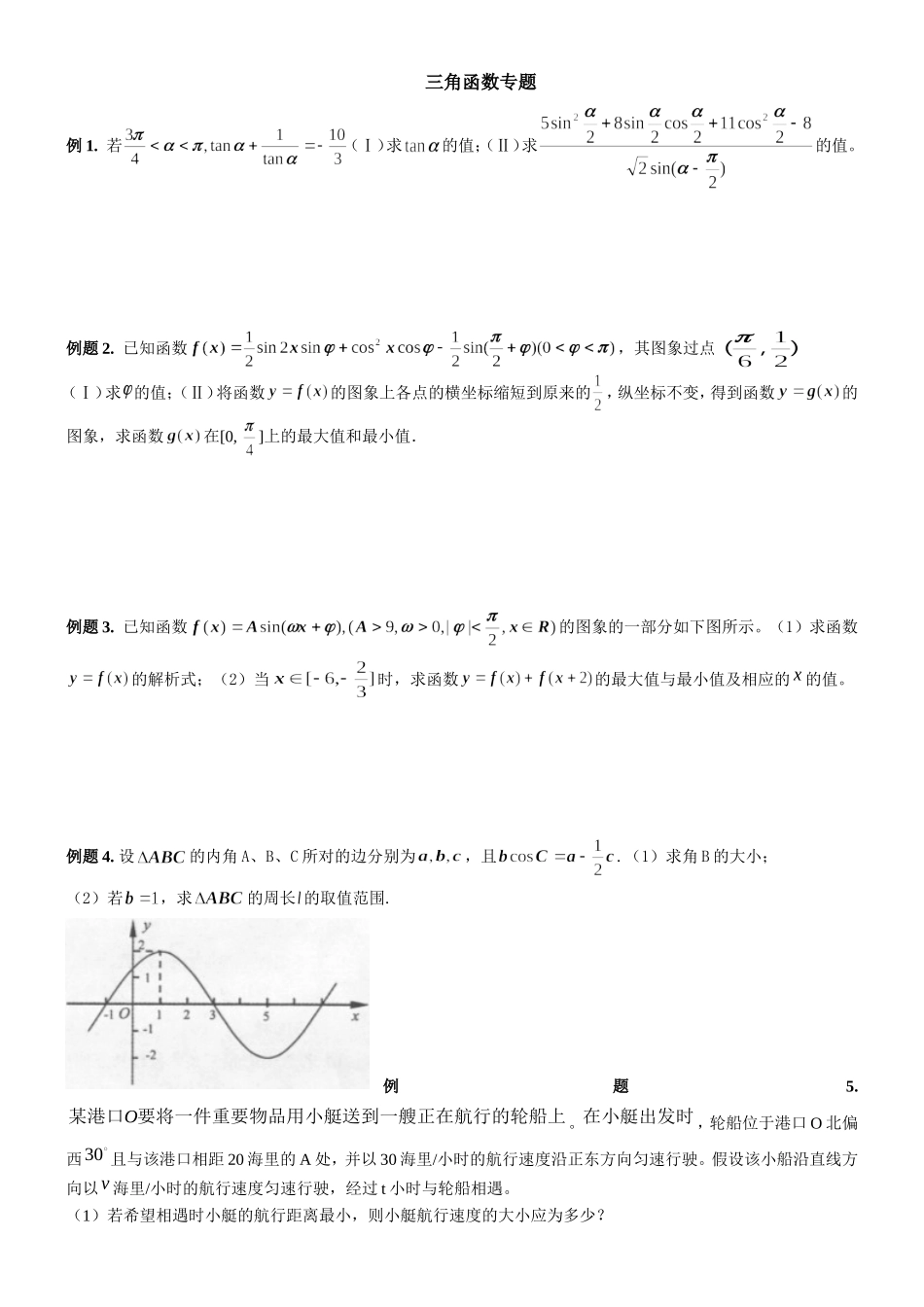
三角函数专题例1.若(Ⅰ)求的值;(Ⅱ)求的值。例题2.已知函数,其图象过点(Ⅰ)求的值;(Ⅱ)将函数的图象上各点的横坐标缩短到原来的,纵坐标不变,得到函数的图象,求函数在[0,]上的最大值和最小值.例题3.已知函数的图象的一部分如下图所示。(1)求函数的解析式;(2)当时,求函数的最大值与最小值及相应的x的值。例题4.设的内角A、B、C所对的边分别为,且.(1)求角B的大小;(2)若,求的周长的取值范围.例题5.O某港口要将一件重要物品用小艇送到一艘正在航行的轮船上。在小艇出发时,轮船位于港口O北偏西30且与该港口相距20海里的A处,并以30海里/小时的航行速度沿正东方向匀速行驶。假设该小船沿直线方向以v海里/小时的航行速度匀速行驶,经过t小时与轮船相遇。(1)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?(2)假设小艇的最高航行速度只能达到30海里/小时,试设计航行方案(即确定航行方向与航行速度的大小),使得小艇能以最短时间与轮船相遇,并说明理由。例题6.已知向量()和=(),∈[π,2π].(1)求的最大值;(2)当=时,求的值三角函数练习1.已知函数(1)求函数的最小正周期和最值;(2)指出图像经过怎样的平移变换后得到的图像关于原点对称。2.已知函数。(1)求函数的最小正周期及在区间上的最大值和最小值:(2)若,求的值。3.已知函数为偶函数,且函数图象的两相邻对称轴间的距离为(Ⅰ)求f()的值;(Ⅱ)将函数的图象向右平移个单位后,再将得到的图象上各点的横坐标舒畅长到原来的4倍,纵坐标不变,得到函数的图象,求g(x)的单调递减区间.4.已知,,求5.设中分别是角的对边,且.(Ⅰ)求sinA的值;(Ⅱ)求的值.6.已知,为的最小正周期,,且.求的值.7.在中,分别是角的对边,且满足(Ⅰ)求角的大小;(Ⅱ)若,求的最小值.8.中,分别是角的对边,(1)求;(2)若,求.w.9.在中,(Ⅰ)求角的大小;(Ⅱ)若ABC△最大边的边长为,求最小边的边长.10.在中,分别是角的对边,其外接圆半径为6,(1)求Bcos;(2)求ABC的面积的最大值。11.已知函数(x∈R)的部分图象如图所示.(1)求的表达式;(2)设求函数g(x)的最小值及相应的x的取值集合.12.已知函数,的图象与x轴的交点中,相邻两个交点之间的距离为,且图象上一个最低点为.(Ⅰ)求的解析式;(Ⅱ)当,求的值域.13.已知:,(Ⅰ)求关于x的表达式,并求的最小正周期;(Ⅱ)若时,的最小值为5,求m的值14.已知向量,设函数.(Ⅰ)若,且,求实数t的值;(Ⅱ)在中,分别是角的对边,若,且的面积为,实数,求边长的值.15.设函数(1)求的最小正周期与单调递减区间;(2)在中,a、b、c分别是角A、B、C的对边,已知,的面积为的值。16.已知,函数(1)求的最小正周期,并求其图象对称中心的坐标;(2)当时,求函数的值域。17.如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶。测量船于水面A处测得B点和D点的仰角分别为,,于水面C处测得B点和D点的仰角均为,AC=0.1km。试探究图中B,D间距离与另外哪两点距离相等,然后求B,D的距离(计算结果精确到0.01km,1.414,2.449)三角测试1.已知函数(1)当时,写出函数的单调递减区间(2)设的最小值是-2,是大值是,求实数的值2.已知函数44cos2cos21()sin()sin()44xxfxxx(Ⅰ)求11()12f的值;(Ⅱ)当[0,)4x时,求1()()sin22gxfxx的最大值和最小值。3.在△ABC中,a,b,c分别为内角A,B,C的对边,且(Ⅰ)求A的大小(Ⅱ)求的最大值.4.已知向量(1)若求x的值;(2)函数,若恒成立,求实数c的取值范围.