高中数学立体几何中的向量方法课件人教版选修二 课件VIP免费

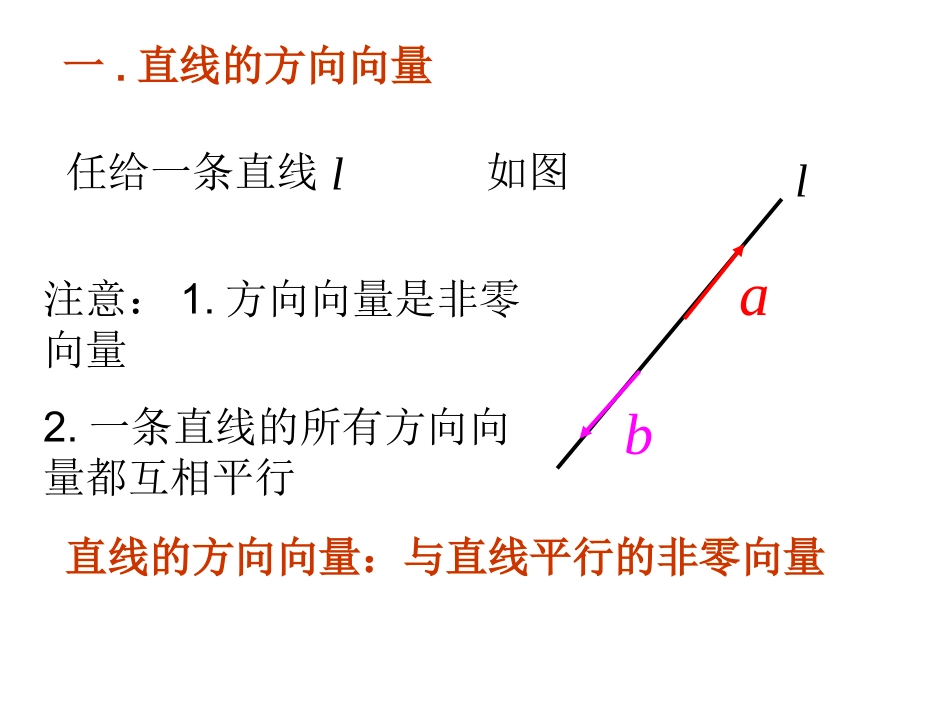
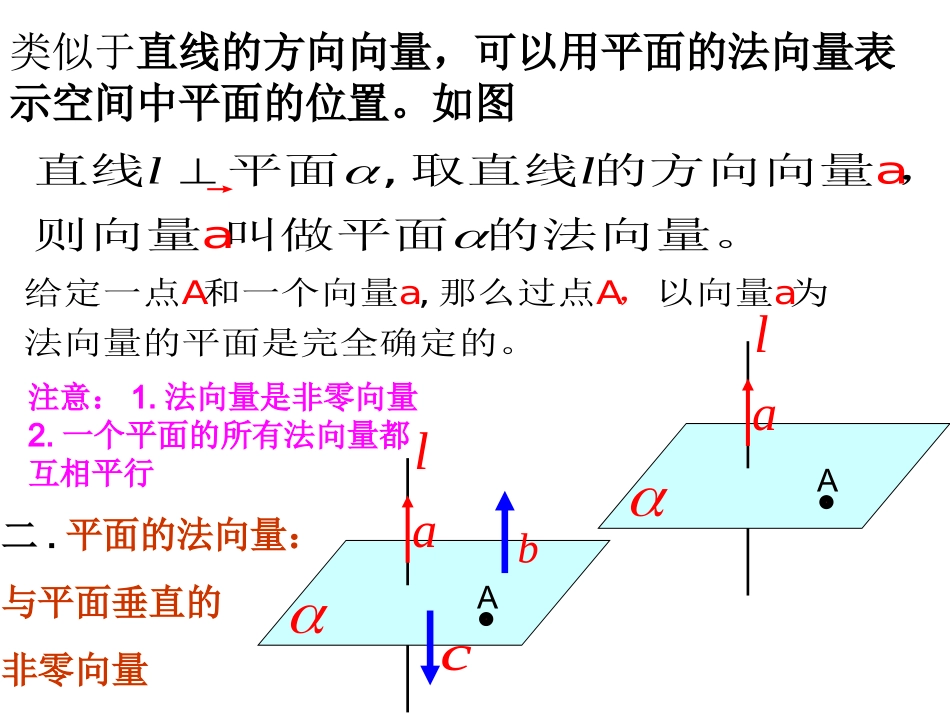
一.直线的方向向量任给一条直线如图labl注意：1.方向向量是非零向量2.一条直线的所有方向向量都互相平行直线的方向向量：与直线平行的非零向量类似于直线的方向向量，可以用平面的法向量表示空间中平面的位置。如图lla直线平面,取直线的方向向量，则向量叫做平面的a法向量。Ala给定一点和一个向量,那么过点以向量为法向量的平面是完全AaA，a确定的。注意：1.法向量是非零向量2.一个平面的所有法向量都互相平行Alabc二.平面的法向量：与平面垂直的非零向量设直线,lm的方向向量分别为,ab，平面,的法向量分别为,uv，则l∥ma∥bakb；线面平行∥u∥v.ukv注意：这里的线线平行包括线线重合，线面平行包括线在面内，面面平行包括面面重合.线线平行l∥au0au；面面平行三、平行关系：设直线,lm的方向向量分别为,ab，平面,的法向量分别为,uv，则线线垂直线面垂直⊥u⊥v.0vul⊥ma⊥b0ab；l⊥a∥uaku；面面垂直四、垂直关系：111222222,,0,//abcabcauabc当时111222(,,),(,,),aabcuabc若则121212//,,.lauakuakabkbckc设直线,lm的方向向量分别为,ab，平面,的法向量分别为,uv，则两直线l,m所成的角为(02≤≤),cosabab；直线l与平面所成的角为(02≤≤),sinauau；二面角─l─的大小为(0≤≤),cos.uvuv以上思考在今后的解题中会经常用到,注意体会.五、夹角：lamb，的夹角为ml,||||||cosbabalambula,l的夹角为，||||||)2cos(uauaula||cos()2||||auau或||sin||||auau则uv，的夹角为,||||||cosvuvul两个平面的法向量与的夹角（或其补角）就是二面角的平面角。uvuv，的夹角为,||||||cosvuvul两个平面的法向量与的夹角（或其补角）就是二面角的平面角。uv应用（一）线线角法1：直接成角（将其中一条直线平移到与另一条直线相交），再求角的大小。（一般构造三角形求角的大小）法2：利用两直线对应向量的数量积求角。61-1111111PABCD-ABCDACBA()A.30B.45C.60D.90例导航正方体中，异面直线与所成的角等于C1D1B1A1CDABF1E1C1B1A1D1DABCyzxO解：设正方体的棱长为1，如图建立空间直角坐标系，则Oxyz13(1,1,0),1,,1,4BE11(0,0,0),0,1.4DF，1311,,1(1,1,0)0,,1,44BE�例2如图,在正方体中，，求与所成的角的余弦值.1111ABCDABCD11BE11114ABDF1BE1DF1110,1(0,0,0)0,1.44DF�，，1111150011,4416BEDF�111717||,||.44BEDF�111111151516cos,.17||||171744BEDFBEDFBEDF���课本P96-例5应用（二）线面角法1：直接成角（根据定义找出斜线的射影成角。再利用三角形求角的大小）法2：利用平面的法向量与直线的方向向量的数量积求角。3例如图,四棱锥P-ABCD,PA垂直于正方形ABCD所在的平面，PA=6,AD=1,求PC与平面ABCD所成的角。BDACPABCD1A1B1C1DMxyzBCD1A1B1C1DMN|||||||sin|nADnAD解：如图建立坐标系A-xyz,则(0,0,0),A)6,2,6(M可得由,51NA)3,4,0(N).3,4,0(),6,2,6(NAMA由的法向量设平面),,,(zyxn00nNAnMA0340626zyzyx即在长方体中，ADANM求与平面所成的角的正弦值.例1：1111ABCDABCD1112,MBCBM为上的一点,且1NAD点在线段上，15,AN,61AA,8,6ADABABCD1A1B1C1DMNxyzBCD1A1B1C1DMN)34,1,1(n得,34343)34(118|0810|222(0,8,0),AD�又ADANM与平面所成角的正弦值是34343|||||||sin|nDAnDA在长方体中，ADANM求与平面所成的角的正弦值.练习：1111ABCDABCD1112,MBCBM为上的一点,且1NAD点在线段上，15,AN,61AA,8,6ADAB应用（三）面面角法1：直接成角（根据定义找出二面角的平面角。再利用三角形求角的大小）法2：利用两平面的法向量的数量积求角。1111114ABCD-ABCDAB=2AA=1A-BD-A例如图，在正四棱柱中，，，求二面角的大小。CDBAC1D1A1B1