高中数学(直线与抛物线的位置关系)课件 新人教版选修2-1 课件VIP免费

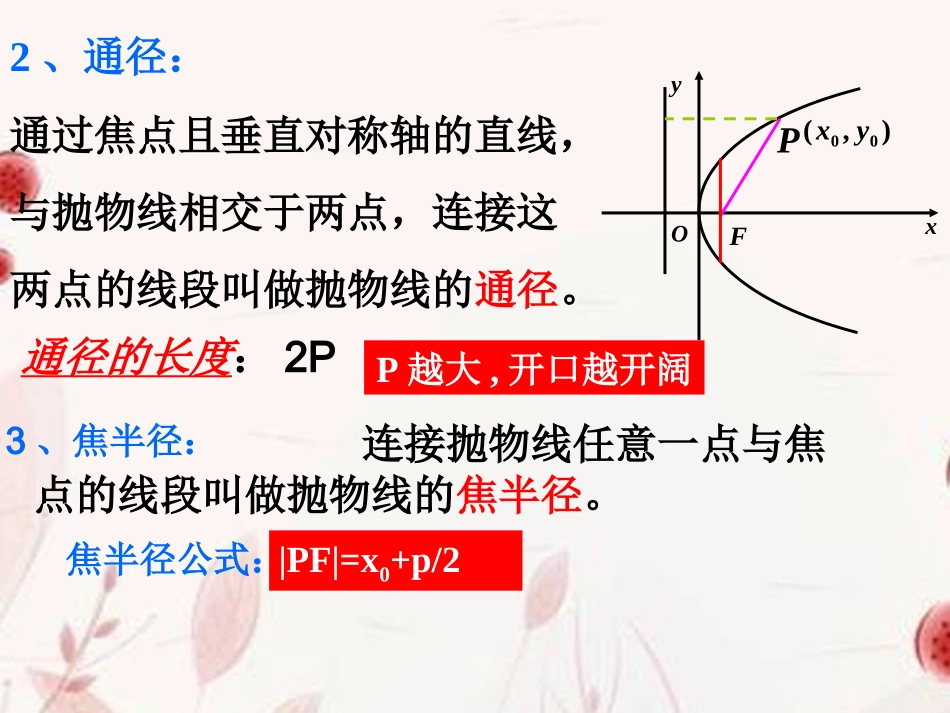
直线与抛物线的位置关系复习：1、抛物线的几何性质图形方程焦点准线范围顶点对称轴elFyxOlFyxOlFyxOlFyxOy2=2px（p>0）y2=-2px（p>0）x2=2py（p>0）x2=-2py（p>0）)0,2(pF)0,2(pF)2,0(pF)2,0(pF2px2px2py2pyx≥0yR∈x≤0yR∈y≥0xR∈y≤0xR∈(0,0)x轴y轴12、通径：通过焦点且垂直对称轴的直线，与抛物线相交于两点，连接这两点的线段叫做抛物线的通径。|PF|=x0+p/2xOyFP通径的长度：2PP越大,开口越开阔3、焦半径：连接抛物线任意一点与焦点的线段叫做抛物线的焦半径。焦半径公式：),(00yx通过焦点的直线，与抛物线相交于两点，连接这两点的线段叫做抛物线的焦点弦。xOyFA4.焦点弦：焦点弦公式：),(11yx下面请大家推导出其余三种标准方程抛物线的焦点弦公式。B),(22yx12pxx方程图形范围对称性顶点焦半径焦点弦的长度y2=2px（p＞0）y2=-2px（p＞0）x2=2py（p＞0）x2=-2py（p＞0）lFyxOlFyxOlFyxOx≥0yR∈x≤0yR∈xR∈y≥0y≤0xR∈lFyxO12pxx12()pxx12pyy12()pyy02px02px02py02py关于x轴对称关于x轴对称关于y轴对称关于y轴对称（0,0）（0,0）（0,0）（0,0）xOyFA),(11yxB),(22yx122pxxPAB若为的中点，则P到准线的距离为多少？思考：直线和抛物线的位置关系有哪些：yFxOll1来表示上述关系方程和抛物线如何用直线方程pxybkxy22归纳方法：1.联立方程组，并化为关于x或y的一元方程；2.考察二次项的系数是否为0，①若为0，则直线与抛物线的对称轴平行，直线与抛物线有且仅有一个交点；②若不为0，则进入下一步.3.考察判别式⊿>0直线与抛物线相交；⊿=0直线与抛物线相切；⊿<0直线与抛物线相离.例1.已知抛物线y2=4x,过定点A(-2,1)的直线l的斜率为k,下列情况下分别求k的取值范围：1.l与抛物线有且仅有一个公共点；2.l与抛物线恰有两个公共点；3.l与抛物线没有公共点.直线与抛物线的关系)2(1xky解：设直线方程为得由)2(142xkyxy02442kyky合题意时，上式只有一解，符当0)1(k016168002kkk得时由当1313kk或即13130kkk或或所以只有一个交点时有）当有两个交点时，则（200k01313kk且解得当没有交点时，有)3(00k1313kk或解得例2.已知抛物线：,直线l:4x-y-6=0,求抛物线上的点P到直线l的最短距离.yxO022yxP解：设抛物线上一点），（22,xx的距离为到则lp1462422xxd174)1(22x174)1(22x时所以1x174mind1717417174的最短距离为到直线综上：点lP你还有其它解法吗例2.已知抛物线：,直线l:4x-y-6=0,求抛物线上的点P到直线l的最短距离.yxO022yx:ml直线平行且与抛物线相切的法二：设与直线04cyx得由02042yxcyx0422cxx0816c2c即的距离与直线lm2221BAccd17)6(217174例23.已知抛物线x=2y,过点Q(0,-2)作一直线交抛物线于A、B两点，试求弦AB中点的轨迹方程.),(),,(,2:2211yxByxAkxyAB解：设直线0422222kxxyxkxy得联立,221kxx则)2()2(2121kxkxyy424)(221kxxk),yxPAB（中点设2422kykx2422xy22xy即)220(kk或得)22(xx或2:244lyxyxAB如图，已知直线交抛物线与、两点，试在抛物线AOB这段曲线上求一点P，使PAB的面积最大，并求出这个最大面积。22:2222041480214952105myxcyxcyxcyxccmd设和抛物线相切且和已知直线平行的直线为由得即直线与已知直线距离2211221212454024(,),(,),+=545251635yxxxyxAxyBxyxxxxAB解：由得设则，12724SABd