高中数学：31(空间向量坐标)课件(苏教版选修2-1) 课件VIP免费

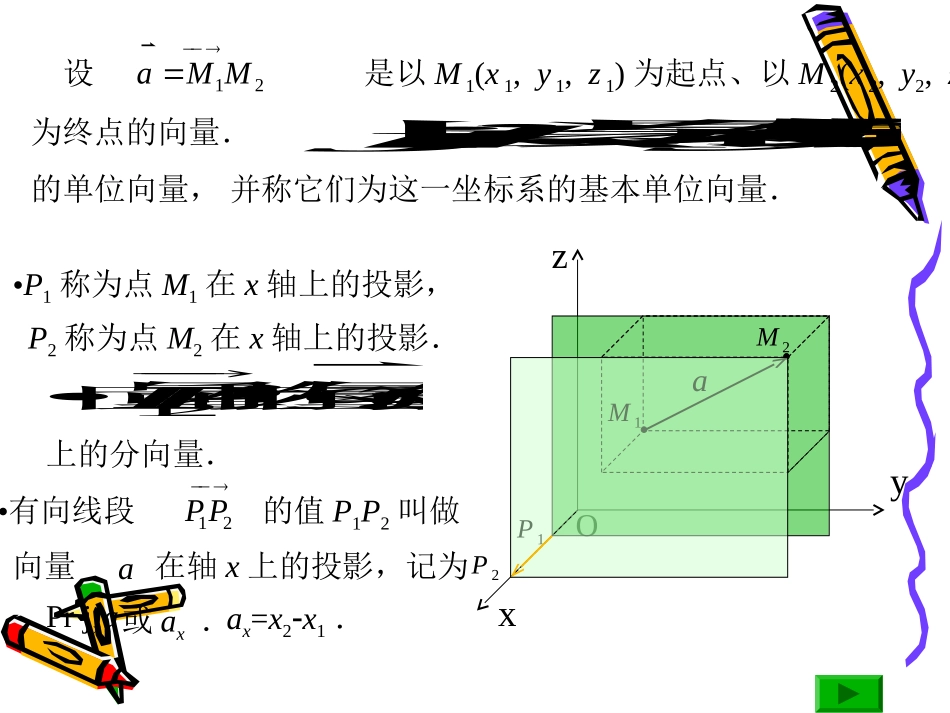
空间向量的坐标一、向量在坐标轴上的分向量与向量的坐标二、向量的模与方向余弦的坐标表示点在坐标轴上的投影、向量在坐标轴上的分向量和投影向量的分解式、向量的坐标、向量的坐标表示式利用坐标进行向量的加减和数乘、利用坐标判断两个向量的平行两个向量的夹角、投影定理向量的方向角、向量的方向余弦向量的模的坐标表示方向余弦的坐标表示、单位向量的表示数轴上的有向线段的值：设在数轴u上点A、B的坐标分别为u1、u2，记作AB．则称数值u2u1即AB=u2u1．则显然有u2u1uO1AB一、向量在坐标轴上的分向量与向量的坐标AB为数轴u上有向线段的值，AB设是与数轴u同方向的单位向量，e(u2u1)．eeP1为终点的向量．的单位向量，并称它们为这一坐标系的基本单位向量．Oxyz•P1称为点M1在x轴上的投影，P2称为点M2在x轴上的投影．上的分向量．M1M2P2a或ax．ax=x2x1．设是以M1(x1,y1,z1)为起点、以M2(x2,y2,z2)21MMa以、、分别表示与x轴、y轴、z轴同向ijk•向量称为向量在x轴21PPa•有向线段的值P1P2叫做21PP向量在轴x上的投影，记为aaxjPr•Q1称为点M1在y轴上的投影，Q2称为点M2在y轴上的投影．上的分向量．xyzP2P1OM1M2a或ay．ay=y2y1．Q2Q1为终点的向量．的单位向量，并称它们为这一坐标系的基本单位向量．设是以M1(x1,y1,z1)为起点、以M2(x2,y2,z2)21MMa以、、分别表示与x轴、y轴、z轴同向ijk•向量称为向量在y轴a21QQ•有向线段的值Q1Q2叫做21QQ向量在轴y的投影，记为aayjPr•R1称为点M1在z轴上的投影，R2称为点M2在z轴上的投影．上的分向量．xyzM2P2P1Q2Q1OaM1或az．az=z2z1．R2R1为终点的向量．的单位向量，并称它们为这一坐标系的基本单位向量．设是以M1(x1,y1,z1)为起点、以M2(x2,y2,z2)21MMa以、、分别表示与x轴、y轴、z轴同向ijk•向量称为向量在z轴21RRa•有向线段的值R1R2叫做21RR向量在轴z的投影，记为aazjPrOxyzM1M2P2P1Q2Q1R2R1a21PP21QQ21RR为终点的向量．的单位向量，并称它们为这一坐标系的基本单位向量．设是以M1(x1,y1,z1)为起点、以M2(x2,y2,z2)21MMa以、、分别表示与x轴、y轴、z轴同向ijkax(x2x1)、iiay(y2y1)、jjaz(z2z1)，kkOxyzM1M2P2P1Q2Q1R2R1aaa起点为M1(x1，y1，z1)而终点为M2(x2，y2，z2)的向量21PP21QQ21RRax(x2x1)、iiay(y2y1)、jjaz(z2z1)，kk(x2x1)(y2y1)(z2z1)．jkiaxayazia21MMjk此式叫做向量的坐标表示式．a并记{ax、ay、az}，a上式称为向量按基本单位向量的分解式．a向量在三个坐标轴上的投影ax、ay、az叫做向量的坐标，aa注意：向量在坐标轴上的分向量与向量在坐标轴上的投影(即向量的坐标)有本质的区别，向量在坐标轴上的投影是三个数ax，ay，az，而向量在坐标轴上的分向量是三个向量ax、ay、az．ijk利用向量的坐标进行向量的加减和数乘：则{axbx，ayby，azbz}．{axbx，ayby，azbz}．{ax，ay，az}．设a{ax，ay，az}，b{bx，by，bz}．，即aaxiayjazk，bbxibyjbzk，则ab(axiayjazk)(bxibyjbzk)(axbx)i(ayby)j(azbz)kbaa(axiayjazk)(ax)i(ay)j(az)k利用向量的坐标判断两个向量的平行：设a{ax，ay，az}0，b{bx，by，bz}，则b//aba，则即b//a{bx，by，bz}{ax，ay，az}，于是zzyyxxababab．即于是例1设A(x1，y1，z1)和B(x2，y2，z2)为两已知点，而在AB解设所求点为M(x，y，z)，则{xx1，yy1，zz1}{x2x，y2y，z2z}，{x，y，z}{x1，y1，z1}{x2，y2，2}{x，y，z}，BAMxyzO直线上的点M分有向线段AB为两个有向线段AM与MB，使它们的值的比等于某数(1)，即MBAM...