高中数学 111正弦定理课件(二) 新人教A版必修5 课件VIP免费

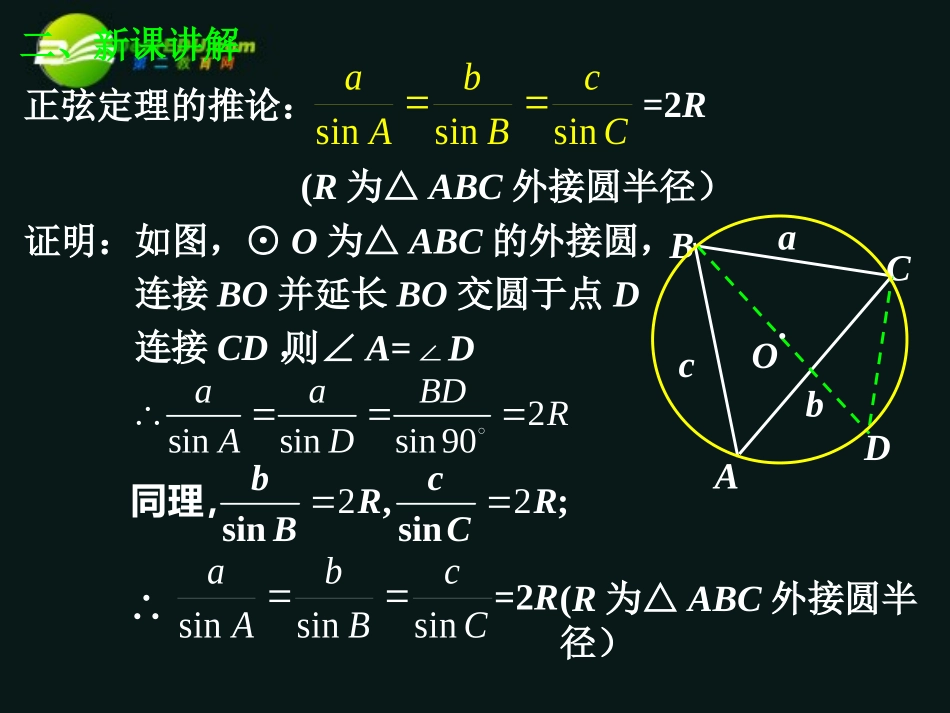
一、复习abcsinAsinBsinC1.正弦定理:在一个三角形中，各边和它所对角的正弦的比相等。即:BCAabc2.可以用正弦定理解决的三角问题：题型一：知两角及一边，求其它的边和角题型二：知两边及其中一边对角，求其他边和角证明：如图，⊙O为△ABC的外接圆，正弦定理的推论：ABCD.ObacsinsinsinabcABC=2R(R为△ABC外接圆半径）2sinsinsin90aaBDRAD22,;sinsinbcRRBC同理，∴sinsinsinabcABC=2R(R为△ABC外接圆半径）二、新课讲解则∠A=∠D连接BO并延长BO交圆于点D连接CD，等腰三角形或直角三角形正弦定理的推论：sinsinsinabcABC=22RR(R为△ABC外接圆半径）222sin,sin,sinaRAbRBcRC222sin,sin,sinabcABCRRRsin:sin:sin::ABCabc二、新课讲解>45º或135º三、例题讲解例1在△ABC中，A=32.0º，B=81.5º，a=42.9，解此三角形．（精确到0.1cm）解:根据三角形的内角和定理：C=180º-(A+B)=66.2º由正弦定理可得429818801320ooasinB.sin.b.(cm)sinAsin.由正弦定理可得429662741320ooasinC.sin.c.(cm)sinAsin.应用正弦定理解三角形题型一:已知两角和任意一边，求出其他两边和一角三、例题讲解解:由正弦定理可得28400899920obsinAsinsinB.a0180ooB64,oB当时C=180º-(A+B)≈76º(1)20763040ooasinCsinc(cm)sinAsinC=180º-(A+B)≈24º20241340ooasinCsinc(cm)sinAsin(2)当B≈116º时，题型二:已知两边和其中一边的对角，求出三角形的另一边和另外两个角.例2.在△ABC中，a=20cm，b=28cm,A=40º，解此三角形．64oB116oB或例3.在△ABC中，A=45º，，解此三角形．64a,b三、例题讲解解:由正弦定理可得018028152ooooBB,B或445047146obsinAsinsinB.a28oB由b＜a，A=45o,可知B＜A∴C=180º-(A+B)≈107º61078145ooasinCsinc.sinAsin题型二:已知两边和其中一边的对角，求出三角形的另一边和另外两个角.例2.在△ABC中，a=20cm，b=28cm,A=40º，解此三角形．若已知a、b、A的值，则解该三角形的步骤如下：（1）先利用求出sinB，从而求出角B；（2）利用A、B求出角C=180o-(A+B)；（3）再利用求出边c.sinsinabABsinsinacAC三、例题讲解题型二:已知两边和其中一边的对角，求出三角形的另一边和另外两个角.注意：求角B时应注意检验！例3在△ABC中,A=45º，,这样的三角形有__个64a,b三、例题讲解1.画∠PAQ=45º2.在AP上取AC=b=43.以C为圆心,a=6为半径画弧,弧与AQ的交点为B45°APQCbBa变式:(1)在△ABC中,A=45º，,这样的三角形有___34a,b(2)在△ABC中,A=45º，,这样的三角形有___224a,b(3)在△ABC中,A=45º，,这样的三角形有___24a,b(4)在△ABC中,A=135º，,这样的三角形有___64a,b(5)在△ABC中,A=135º，,这样的三角形有___34a,b2个1个0个1个0个1已知两边和其中一边的对角时，解斜三角形的各种情况a≥b一解bsinAa无解(一)当A为锐角(二)当A为钝角a>b一解a≤b无解三、例题讲解(三)当A为直角ACbaa>b一解ACbaa≤b无解若已知三角形的两条边及其中一边的对角（若已知a、b、A的值），则可用正弦定理求解，且解的情况如下AA的范围的范围a,ba,b关系关系解的情况解的情况AA为钝角或直角为钝角或直角AA为锐角为锐角aa＞＞bbaa≤≤bbaa＜＜bbsinsinAAaa==bbsinsinAAbbsinsinAA＜＜aa＜＜bb一解一解无解无解无解无解一解一解两解两解aa≥≥bb一解一解2.在△ABC中,由已知条件解三角形,下列有两解的是()A．b=20,A=45º,C=80ºB．a=30,c=28,B=60ºC．a=14,b=16,A=45ºD．a=12,c=15,A=120º四、练习※判断已知两边及其中一边对角的三角形解的个数的基本步骤(适合填空或选择题)：（1）判断已知角A的类型；（钝、直、锐）（2）判断已知两边a、b的大小关系；（3）判断a与bsinA的大小关系.C1.在△ABC中，∠A,∠B,∠C所对的边分别是a,b,c，则下列关系一定成立的是()A．a>bsinAB．a=bsinAC．a