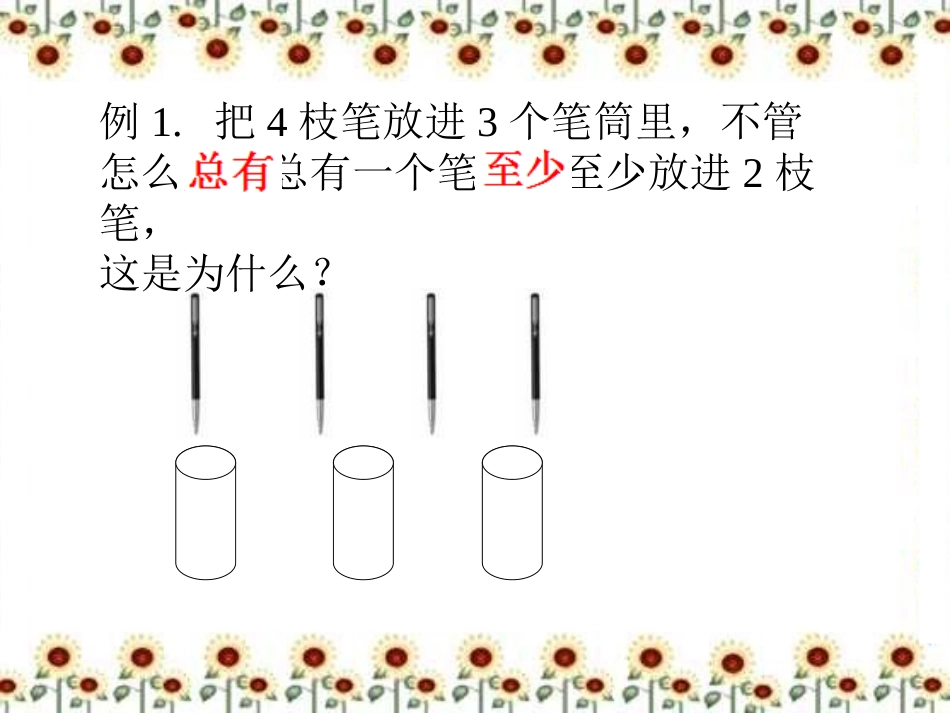
义务教育教科书人教版六年级下册第五单元新洲区李集街得胜小学郑梦霞摸扑克牌例1.把4枝笔放进3个笔筒里,不管怎么放,总有一个笔筒里至少放进2枝笔,这是为什么?不管怎么放,总有一个杯子里至少有2支笔假设每个笔筒里先放1支,那么剩下的1支无论放在哪个笔筒,那个笔筒就有2支。把5支笔放进4个笔筒里,总有一个笔筒里至少有2支笔。这句话还成立吗?成立把7支笔放进6个笔筒里呢?把10支笔放进9个笔筒里呢?......把100支笔放进99个笔筒里呢?笔的支数比笔筒数多1,不管怎么放,总有一个笔筒里至少有2支笔。8只鸽子飞回7个鸽巢,10只苹果放进9个抽屉里,总有一个鸽巢至少飞进了2只鸽子。总有一个抽屉至少放了2个苹果。1、假设有12个老师,每人一种属相,那么剩下的一个人,无论放到哪一类,总会有两个人的属相相同。2、5只鸽子飞进了3个鸽笼,总有一个鸽笼至少飞进了2只鸽子。为什么?你知道吗?“抽屉原理”最先是由19世纪的德国数学家狄里克雷(Dirichlet)运用于解决数学问题的,所以又称“狄里克雷原理”,也称为“鸽巢原理”。“抽屉原理”的应用却是千变万化的,用它可以解决许多有趣的问题,并且常常能得到一些令人惊异的结果。