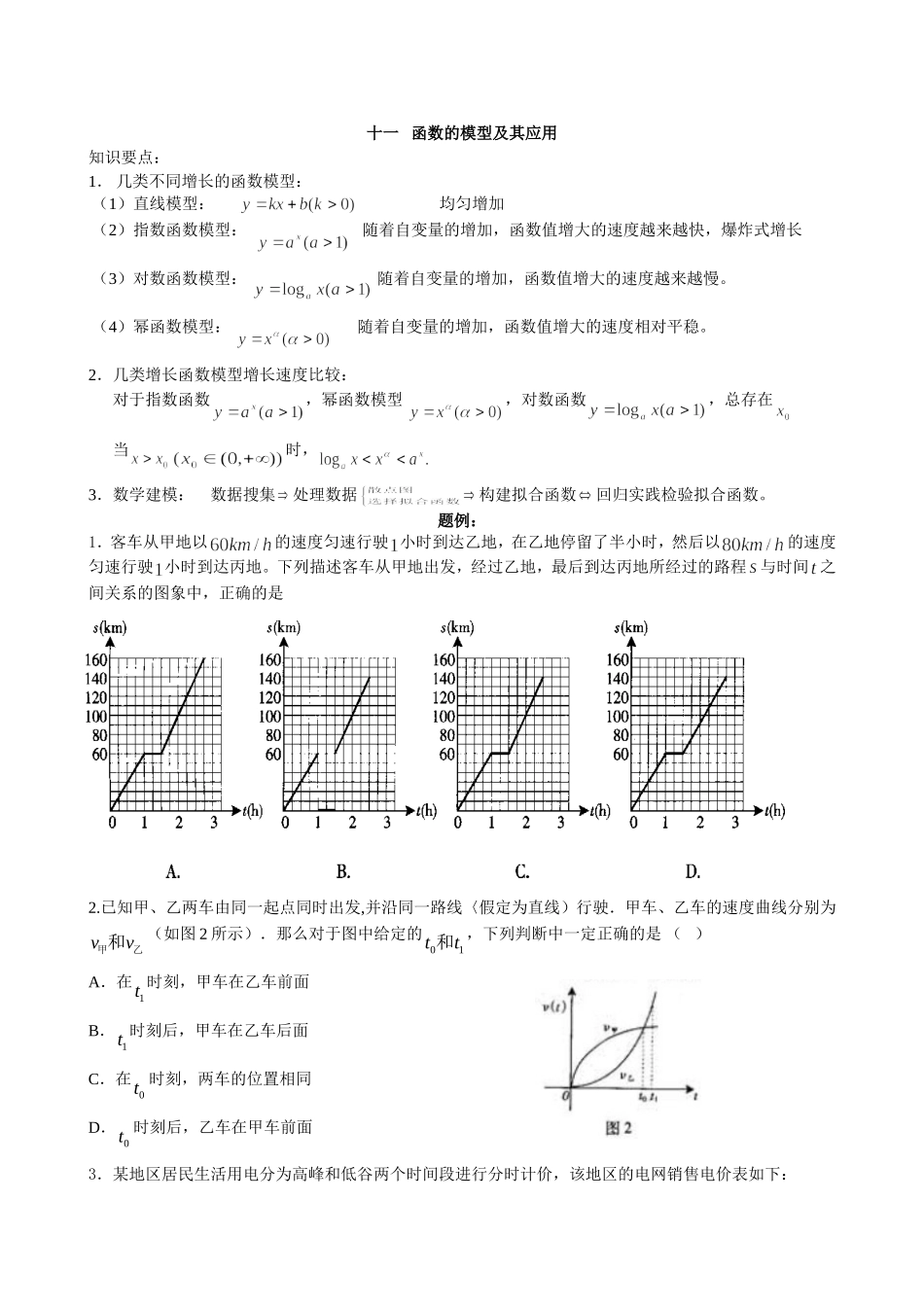
十一函数的模型及其应用知识要点:1.几类不同增长的函数模型:(1)直线模型:均匀增加(2)指数函数模型:随着自变量的增加,函数值增大的速度越来越快,爆炸式增长(3)对数函数模型:随着自变量的增加,函数值增大的速度越来越慢。(4)幂函数模型:随着自变量的增加,函数值增大的速度相对平稳。2.几类增长函数模型增长速度比较:对于指数函数,幂函数模型,对数函数,总存在当时,3.数学建模:数据搜集处理数据构建拟合函数回归实践检验拟合函数。题例:1.客车从甲地以的速度匀速行驶小时到达乙地,在乙地停留了半小时,然后以的速度匀速行驶小时到达丙地。下列描述客车从甲地出发,经过乙地,最后到达丙地所经过的路程与时间之间关系的图象中,正确的是2.已知甲、乙两车由同一起点同时出发,并沿同一路线〈假定为直线)行驶.甲车、乙车的速度曲线分别为vv乙甲和(如图2所示).那么对于图中给定的01tt和,下列判断中一定正确的是()A.在1t时刻,甲车在乙车前面B.1t时刻后,甲车在乙车后面C.在0t时刻,两车的位置相同D.0t时刻后,乙车在甲车前面3.某地区居民生活用电分为高峰和低谷两个时间段进行分时计价,该地区的电网销售电价表如下:高峰时间段用电价格表低谷时间段用电价格表高峰月用电量(单位:千瓦时)高峰电价(单位:元/千瓦时)低谷月用电量(单位:千瓦时)低谷电价(单位:元/千瓦时)50及以下的部分0.56850及以下的部分0.288超过50至200的部分0.598超过50至200的部分0.318超过200的部分0.668超过200的部分0.388若某家庭5月份的高峰时间用电量为200千瓦时,低谷时间段用电量为100千瓦时,则按这种计费方式该家庭本月应付的电费为________元(用数字作答)。4.要在边长为16米的正方形草坪上安装喷水龙头,使整个草坪都能喷洒到水.假设每个喷水龙头的喷洒范围都是关径为6米的圆面,则需安装这种喷水龙头的个数最少是()A.B.C.D.5.为了预防流感,某学校对教室用药熏消毒法进行消毒.已知药物释放过程中,室内每立方米空气中的含药量(毫克)与时间(小时)成正比;药物释放完毕后,与的函数关系式为(为常数),如图所示.据图中提供的信息,回答下列问题:(I)从药物释放开始,每立方米空气中的含药量(毫克)与时间(小时)之间的函数关系式为;(II)据测定,当空气中每立方米的含药量降低到毫克以下时,学生方可进教室,那么药物释放开始,至少需要经过小时后,学生才能回到教室.6.某分公司经销某种品牌产品,每件产品的成本为3元,并且每件产品需向总公司交元()的管理费,预计当每件产品的售价为元()时,一年的销售量为万件.(Ⅰ)求分公司一年的利润(万元)与每件产品的售价的函数关系式;(Ⅱ)当每件产品的售价为多少元时,分公司一年的利润最大,并求出的最大值.解:(Ⅰ)分公司一年的利润(万元)与售价的函数关系式为:.(Ⅱ).令得或(不合题意,舍去).,.在两侧的值由正变负.所以(1)当即时,.O0.11(毫克)(小时)(2)当即时,,所以答:若,则当每件售价为9元时,分公司一年的利润最大,最大值(万元);若,则当每件售价为元时,分公司一年的利润最大,最大值(万元).7.水库的蓄水量随时间而变化,现用t表示时间,以月为单位,年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于t的近似函数关系式为V(t)=(Ⅰ)该水库的蓄水量小于50的时期称为枯水期.以i-1<t<i表示第i月份(i=1,2,…,12),问一年内哪几个月份是枯水期?(Ⅱ)求一年内该水库的最大蓄水量(取e=2.7计算).解:(Ⅰ)①当0<t10时,V(t)=(-t2+14t-40)化简得t2-14t+40>0,解得t<4,或t>10,又0<t10,故0<t<4.②当10<t12时,V(t)=4(t-10)(3t-41)+50<50,化简得(t-10)(3t-41)<0,解得10<t<,又10<t12,故10<t12.综合得0