导数的概念及运算VIP免费

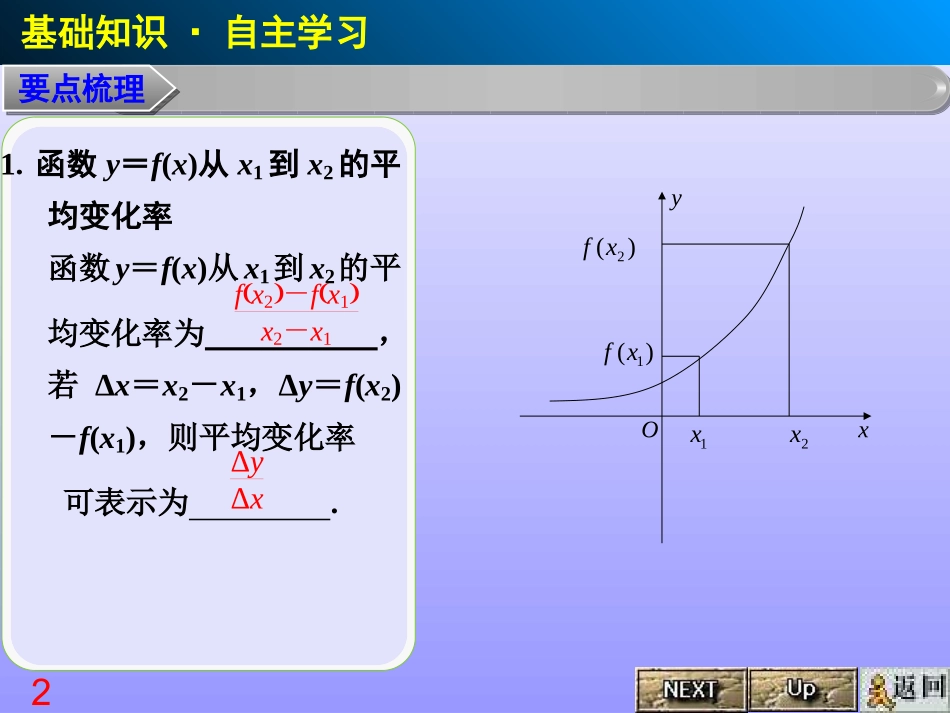
1导数的概念及运算导数的概念及运算xyO0xxx0)(0xxf)(0xf21．函数y＝f(x)从x1到x2的平均变化率函数y＝f(x)从x1到x2的平均变化率为，若Δx＝x2－x1，Δy＝f(x2)－f(x1)，则平均变化率可表示为.基础知识·自主学习要点梳理fx2－fx1x2－x1ΔyΔxxyO1x2x)(2xf)(1xf32．函数y＝f(x)在x＝x0处的导数函数y＝f(x)在x＝x0处的瞬时变化率＝为函数y＝f(x)在x＝x0处的导数，记作f′(x0)，即f′(x0)＝limΔx→0ΔyΔx＝.基础知识·自主学习要点梳理limΔx→0fx0＋Δx－fx0ΔxlimΔx→0ΔyΔxlimΔx→0fx0＋Δx－fx0Δx函数y＝f(x)在x＝x0处的导数刻画了函数y＝f(x)的函数值在x0处随着x的变化而变化快慢的性质.xyO0xxx0)(0xxf)(0xf43．函数f(x)的导函数称函数f′(x)＝为f(x)的导函数，导函数有时也记作y′.基础知识·自主学习要点梳理limΔx→0fx＋Δx－fxΔx(1)函数f(x)在点x0处的导数f′(x0)是一个常数；(2)函数y＝f(x)的导函数，是针对某一区间内任意点x而言的．如果函数y＝f(x)在区间(a，b)内每一点x都可导，是指对于区间(a，b)内的每一个确定的值x0都对应着一个确定的导数f′(x0)．这样就在开区间(a，b)内构成了一个新函数，就是函数f(x)的导函数f′(x)．在不产生混淆的情况下，导函数也简称导数．1．深刻理解“函数在一点处的导数”“导函数”、“导数”的区别与联系54.导数的实际背景：瞬时速度，加速度等等。基础知识·自主学习要点梳理)(tss0ttt0t)()()(lim)(0/0000tsttsttstvt65.导数的几何意义函数f(x)在点x0处的导数f′(x0)的几何意义是在曲线y＝f(x)上点处的．相应地，切线方程为．基础知识·自主学习要点梳理(x0,f(x0))切线的斜率y－f(x0)＝f′(x0)(x－x0)(1)曲线y＝f(x)在点P(x0，y0)处的切线是指P为切点，切线斜率为k＝f′(x0)的切线，是唯一的一条切线．(2)曲线y＝f(x)过点P(x0，y0)的切线，是指切线经过P点．点P可以是切点，也可以不是切点，而且这样的直线可能有多条．2．曲线y＝f(x)“在点P(x0，y0)处的切线”与“过点P(x0，y0)的切线”的区别与联系76.基本初等函数的导数公式基础知识·自主学习要点梳理原函数导函数f(x)＝c(c为常数)f′(x)＝____f(x)＝xα(α为实数)f′(x)＝f(x)＝sinxf′(x)＝f(x)＝cosxf′(x)＝f(x)＝ax(a>0，a≠1)f′(x)＝f(x)＝exf′(x)＝f(x)＝logax(a>0，a≠1)f′(x)＝f(x)＝lnxf′(x)＝f(x)＝tanxf′(x)＝f(x)＝cotxf′(x)＝0cosx－sinxaxlnaex1xlna1xαxα－11cos2x－1sin2x87.导数的运算法则(1)[f(x)±g(x)]′＝；(2)[f(x)·g(x)]′＝；(3)fxgx′＝(g(x)≠0)．8．复合函数的导数复合函数y＝f(g(x))的导数和函数y＝f(u)，u＝g(x)的导数间的关系为y′x＝，即y对x的导数等于的导数与的导数的乘积．基础知识·自主学习要点梳理f′(x)±g′(x)f′(x)g(x)＋f(x)g′(x)f′xgx－fxg′x[gx]2y对uu对xy′u·u′x9例1.是f（x）的导函数，f/（x）的图象如下图,则f（x）的图象只可能是（）DxfAABBCCDD题型分类·深度剖析题型一导数定义的应用10例2.汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车，若把这一过程中汽车的行驶路程s看作时间t的函数，其图像可能是（）stOA．stOstOstOB．C．D．A110xxyo()ygx()yfx例3.已知函数y=f(x),y=g(x)的导数的图像如右图所示，那么y=f(x),y=g(x)的图像可能是（）0xxyo()yfx()ygxA0xxyo()yfx()ygxB0xxyo()yfx()ygxC0xxyo()yfx()ygxDD12【例4】求下列函数的导数：(1)y＝ex·lnx；(2)y＝xx2＋1x＋1x3；(3)y＝sin22x＋π3；(4)y＝ln(2x＋5)．题型分类·深度剖析题型二导数的运算思维启迪解析探究提高13题型分类·深度剖析题型二导数的运算求函数的导数，首先要搞清函数的结构；若式子能化简，可先化简再求导．思维启迪解析探究提高【例4】求下列函数的导数：(1)y＝ex·lnx；(2)y＝xx2＋1x＋1x3；(3)y＝sin22x＋π3；(4)y＝ln(2x＋5)．14【例4】求下列函数的导数：(1)y＝ex·lnx；(2)y＝xx2＋1x＋1x3；(3...