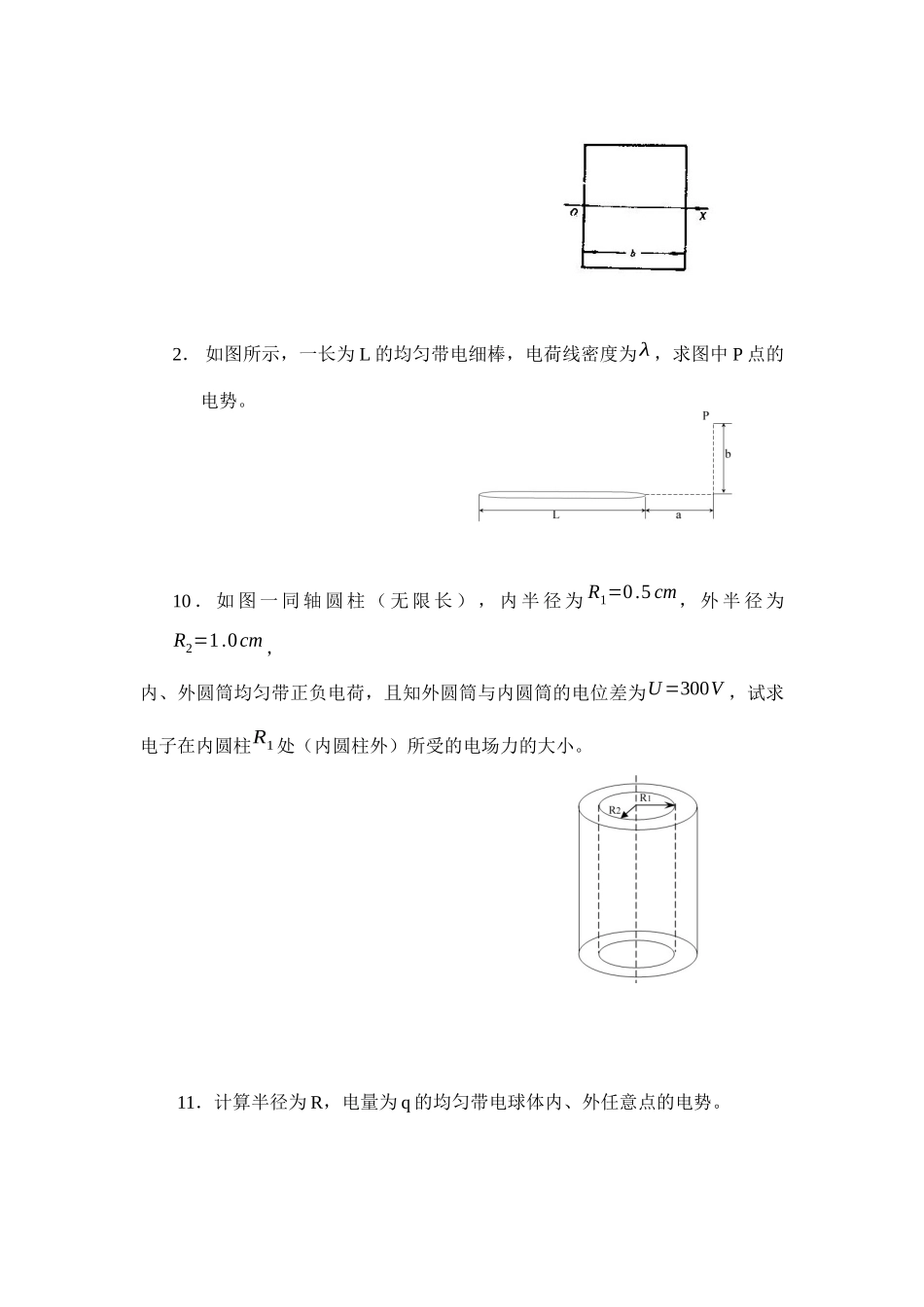
七、静电场1.两个点电荷电量分别为+q和–2q,其间距为d,求:(1)在它们连线中间电势U=0在什么位置?(2)在它们连线上电场强度⃗E=0的点是什么位置?2.如图所示,两个小球质量都是m,都用长为l的细线挂在同一点,若将它们带上相同的电量,平衡时两线夹角为2θ,设小球的半径均可忽略不计,求每个小球所带的电量。3.一半径为R的半圆形细棒,其上均匀带有电荷q,求半圆中心O点的电场强度。4.半径为R的半球面,均匀带有电荷,电荷面密度为σ,求其球心处的电场强度。5.无限大平面开有一个半径为R的圆洞。设平面均匀带电,电荷面密度为σ,求这洞的轴线上离洞心为r处的电场强度。6.有一带电球壳,内外半径分别为a和b,电荷体密度为ρ=Q2πa2r,式中r为球壳内任意点到球心的距离,在球心处放置一点电荷Q,求证球壳区域内场强⃗E与r的大小无关。7.如图所示,虚线为一正立方形的封闭面,已知空间电场的分布为Ex=b√x,Ey=0,Ez=0,正立方形边长a=10cm,b=800N⋅C−1,试求:(1)通过正立方形的电通量;(2)正立方形中所包含的净电荷(ε0=8.85×10−12C2⋅N−1⋅m−2)。1.如图所示,一厚度为b的无限大带电平板,其电荷体密度ρ=kx2(0