等差数列的性质课件 (2)VIP免费

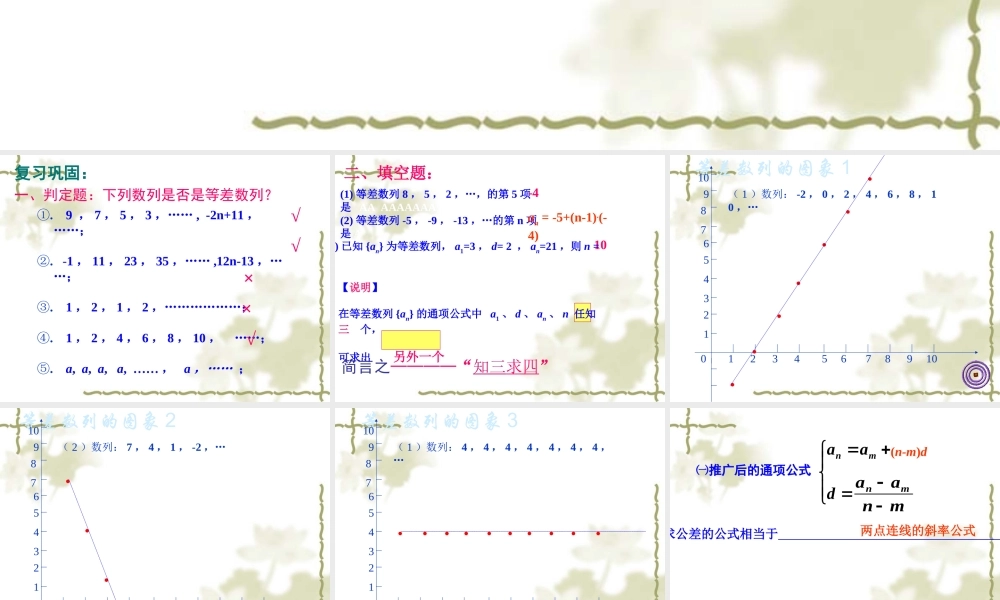
等差数列 一、判定题：下列数列是否是等差数列？①. 9 ， 7 ， 5 ， 3 ，…… , -2n+11 ， ……；②. -1 ， 11 ， 23 ， 35 ，…… ,12n-13 ，……；③. 1 ， 2 ， 1 ， 2 ，………………；④. 1 ， 2 ， 4 ， 6 ， 8 ， 10 ， ……；⑤. a, a, a, a, …… ， a ，…… ；√√√××复习巩固： (1) 等差数列 8 ， 5 ， 2 ，…，的第 5 项是 AA AAAAAAA (2) 等差数列 -5 ， -9 ， -13 ，…的第 n 项是 A -4an = -5+(n-1).(-4)10【说明】 在等差数列 {an} 的通项公式中 a1 、 d 、 an 、 n 任知 三 个，可求出 另外一个二、填空题：简言之————“知三求四”(3) 已知 {an} 为等差数列， a1=3 ， d= 2 ， an=21 ，则 n = 等差数列的图象 1（ 1 ）数列： -2 ， 0 ， 2 ， 4 ， 6 ， 8 ， 10 ，…12345678910123456789100●●●●●●● 等差数列的图象 2（ 2 ）数列： 7 ， 4 ， 1 ， -2 ，…12345678910123456789100●●●● 等差数列的图象 3（ 1 ）数列： 4 ， 4 ， 4 ， 4 ， 4 ， 4 ， 4 ，…12345678910123456789100●●●●●●●●●● ㈠推广后的通项公式 daamn(n-m)dmnaamn【说明】求公差的公式相当于 .两点连线的斜率公式 等差中项 观察如下的两个数之间，插入一个什么数后者三个数就会成为一个等差数列：（ 1 ） 2 ， ， 4 （ 2 ） -1 ， ， 5（ 3 ） -12 ， ， 0 （ 4 ） 0 ， ， 032-60 如果在 a 与 b 中间插入一个数 A ，使 a ， A ， b成等差数列，那么 A 叫做 a 与 b 的等差中项。2baA 【说明】 3. 更一般的情形， an= ， d= 等差数列的性质1. {an} 为等差数列 2. a 、 b 、 c 成等差数列 an+1- an=dan+1=an+dan= a1+(n-1) dan= kn + b（ k 、 b 为常数）am+(n - m) dmnaamnb 为 a 、 c 的等差中项AA2cab2b= a+c4. 在等差数列 {an} 中，由 m+n=p+q am+an=ap+aq注意：上面的命题的逆命题 是不一定成立 的；      1 、已知：数列的通项公式为 an=6n-1 问这个数列是等差数列吗？若是等差数列，其首项与公差分别是多少？分析：由等差数列定义只需判断 an-an-1(n≥2 ， n∈N) 的结果是否为常数。解： an-an-...