指数函数课件VIP免费

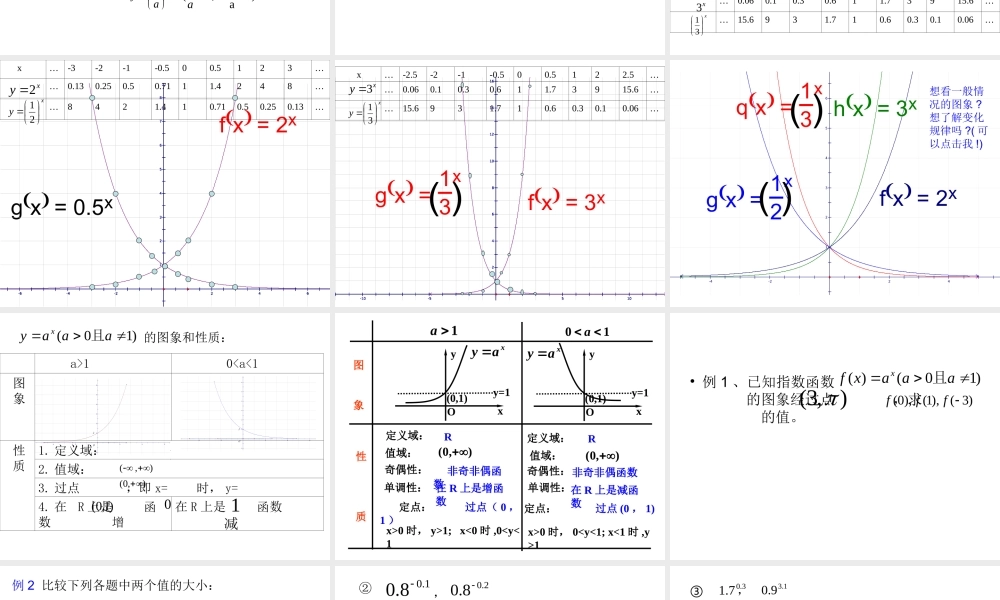
y=ay=axx87654321-1-2-6-4-22468g x  = 12xf x  = 2x 引例 1 ：某种细胞分裂时，由 1 个分裂成 2 个，2 个分裂成 4 个，…… . 1 个这样的细胞分裂 x 次后，得到的细胞个数 y 与 x 的函数关系是什么？分裂次数： 1 ， 2 ， 3 ， 4 ，…，x细胞个数： 2 ， 4 ， 8 ， 16 ，…，y由上面的对应关系可知，函数关系是xy2.引例 2 ：某种商品的价格从今年起每年降低 15% ，设原来的价格为 1 ， x 年后的价格为 y ，则 y 与 x 的 函数关系式为xy85.0 在xy2 ,xy85.0中指数 x 是自变量，底数是一个大于 0 且不等于 1 的常量 . 我们把这种自变量在指数位置上而底数是一个大于 0 且不等于 1 的常量的函数叫做指数函数 .指数函数的定义： 函数)10(aaayx且叫做指数函数，其中 x 是自变量，函数定义域是 R 。 探究 1 ：为什么要规定 a>0, 且 a  1 呢？① 若 a=0 ，则当 x>0 时，xa=0 ；0 时，xa 无意义 . 当 x② 若 a<0 ，则对于 x 的某些数值，可使xa无意义 . 如x)2(，这时对于 x=41， x=21…… 等等，在实数范围内函数值不存在 .③ 若 a=1 ，则对于任何 x  R ，xa =1 ，是一个常量，没有研究的必要性 . 为了避免上述各种情况，所以规定 a>0 且 a1 。 在规定以后，对于任何 x  R ，xa都有意义，且xa >0. 因此指数函数的定义域是 R ，值域是 (0,+∞). 探究 2 ：函数xy32是指数函数吗？指数函数的解析式 y=xa 中，xa的系数是 1.有些函数貌似指数函数，实际上却不是，如kayx  (a>0 且 a1 ， kZ) ； 有些函数看起来不像指数函数，实际上却是，如 xay)1a,0(且a因为它可以化为 xay 1)1a1,01(且a 练习：1 、下列函数中⑴ y= y=4⑵x ⑶y=22x y=3×2⑷x ⑸ y=3x+1⑹y= 是指数函数的是＿＿＿。2 、函数 y=(a2-3a+3)ax是指数函数，则a=_______.23xx3 指数函数的图象和性质：在同一坐标系中分别作出如下函数的图像： xy2xy 21xy3xy 31 列表如下：x2x21 x…-3-2-1-0.500.5123……0.130.250.50.7111.4248……8421.410.710.50.250.13…x3x31 x…-2.5-2-1-0.500.5122.5……0.060.10.30.611.73915.6……15.6931.710.60.30.10.06… 87654321-6-4-2246g x ...