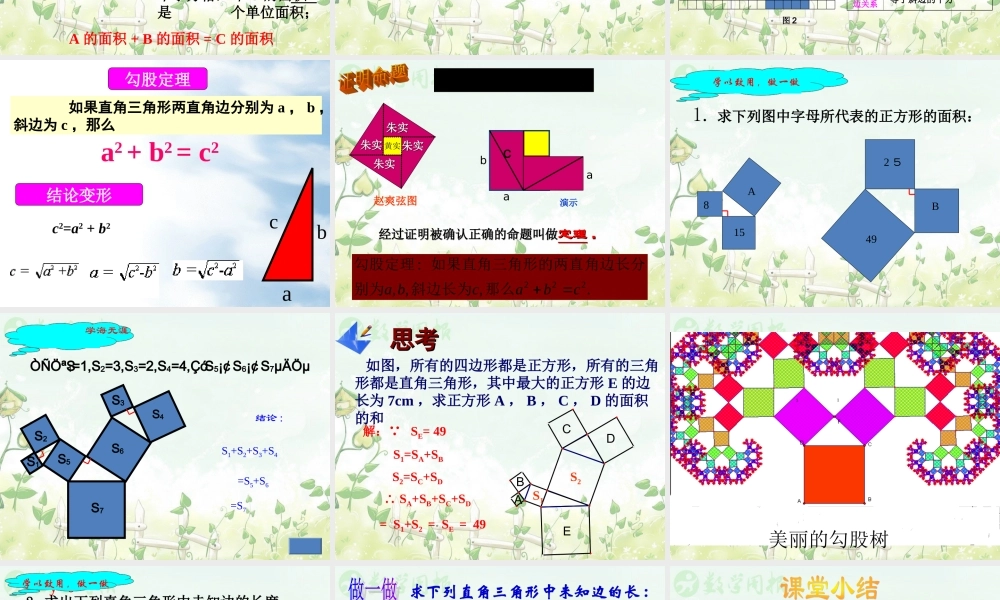
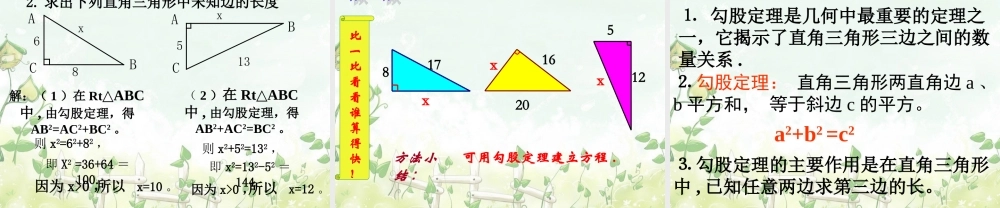
人教版八年级(下册)第十八章勾股定理18.1 勾股定理(第 1 课时)勾股定理勾股弦毕达哥拉斯( 公元前 572---- 前 492年 ),古希腊著名的哲学家、数学家、天文学家。 相传在 2500 年前,毕达哥拉斯有一次在朋友家做客时,发现朋友家用砖铺成的地面中反映了直角三角形三边的某种数量关系,我们一起来观察图中的地面,看看能发现什么。 数学家毕达哥拉斯的发现:A 、 B 、 C 的面积有什么关系?直角三角形三边有什么关系?SA+SB=SC两直边的平方和等于斜边的平方ABC图 1—2ABC( 2 )观察图 1—2 :正方形 A 中含有 个小方格,即 A 的面积是 个单位面积;正方形 B 中含有 个小方格,即 B 的面积是 个单位面积;正方形 C 中含有 个小方格,即 C 的面积是 个单位面积;444488A 的面积 + B 的面积 = C 的面积 因此可知等腰直角三角形有这样的性质:对于任意直角三角形都有这样的性质吗?两直角边的平方和等于斜边的平方看下图ABCA 的面积 ( 单位长度 )B 的面积 ( 单位长度 )C 的面积 ( 单位长度 )图 1图 2A 、 B 、C 面积关系直角三角形三边关系图 1图 2491392534sA+sB=sC 两直角边的平方和等于斜边的平方ABCabcc2=a2 + b2 如果直角三角形两直角边分别为 a , b ,斜边为 c ,那么a2 + b2 = c2勾股定理结论变形黄实朱实朱实朱实朱实朱实朱实朱实朱实ba22:ba 它们的面积和a.,,, 1222cbacba那么斜边长为别为角边长分如果直角三角形的两直命题.,,, :222cbacba那么斜边长为别为角边长分如果直角三角形的两直勾股定理经过证明被确认正确的命题叫做经过证明被确认正确的命题叫做定理定理 ..演示C赵爽弦图815A49B2 51. 求下列图中字母所代表的正方形的面积:y=0学以致用,做一做S1S2S3S4S5S6S7ÒÑÖªS1=1,S2=3,S3=2,S4=4,ÇóS5¡¢ S6¡¢ S7µÄÖµ结论 :S1+S2+S3+S4=S5+S6=S7y=0学海无涯EDCBA 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形 E 的边长为 7cm ,求正方形 A , B , C , D 的面积的和思考思考S1S2解: SE= 49S1=SA+SBS2=SC+SD ∴ SA+SB+SC+SD = S1+S2 = SE = 4911美丽的勾股树y=02. 求出下列直角三角形中未知边的长度68x5x13学以致用,做一做解:( 1 )在 Rt ABC△中 , 由勾股定理,得AB2=AC2+BC2 。即 X2 =36+64 =100.则 x2=62+82 ,所以 x=10 。因为 x>...