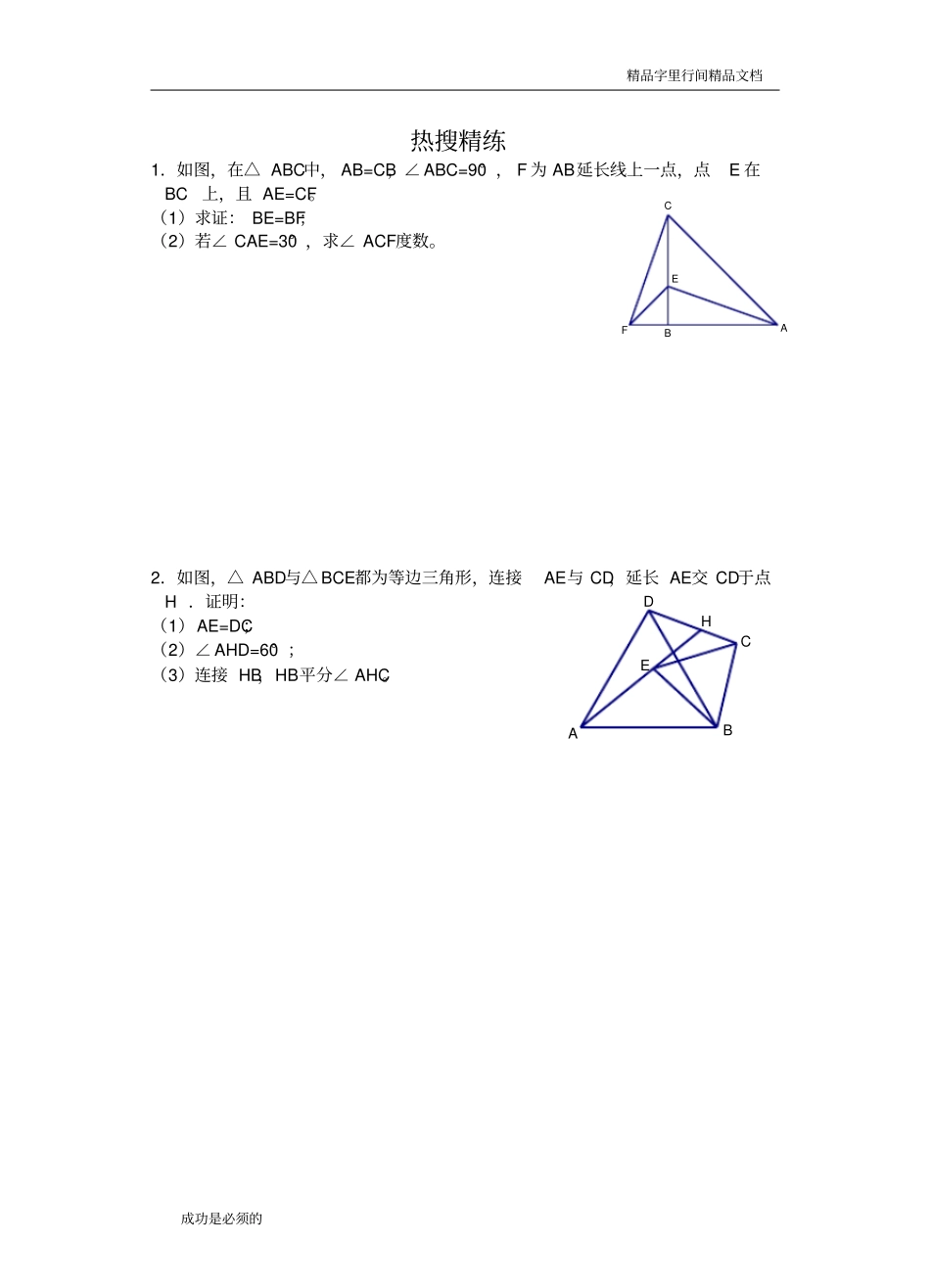
精品字里行间精品文档成功是必须的EADBCEADBCEDCBA图3图21图OHGABCDMPDECBA手拉手模型模型手拉手如图,△ ABC是等腰三角形、△ADE是等腰三角形,AB=AC,AD=AE,∠BAC=∠DAE= 。结论:△ BAD≌△ CAE。模型分析手拉手模型常和旋转结合,在考试中作为几何综合题目出现。模型实例例 1.如图,△ ADC与△ GDB都为等腰直角三角形,连接AG、CB,相交于点H,问:( 1)AG与 CB是否相等?(2)AG与 CB之间的夹角为多少度?3.在线段 AE同侧作等边△ CDE(∠ ACE<120° ),点 P 与点 M分别是线段BE 和 AD的中点。求证:△ CPM是等边三角形。精品字里行间精品文档成功是必须的FECBAHDECBA热搜精练1.如图,在△ ABC中, AB=CB,∠ ABC=90° , F 为 AB延长线上一点,点E 在 BC上,且 AE=CF。(1)求证: BE=BF;(2)若∠ CAE=30° ,求∠ ACF度数。2.如图,△ ABD与△ BCE都为等边三角形,连接AE与 CD,延长 AE交 CD于点 H .证明:(1)AE=DC;(2)∠ AHD=60° ;(3)连接 HB,HB平分∠ AHC。精品字里行间精品文档成功是必须的BADCPE3图BDAEC图 21图PDECBA3.将等腰 Rt△ABC和等腰 Rt△ADE按图①方式放置,∠A=90° , AD边与 AB边重合, AB=2AD=4。将△ ADE绕点 A逆时针方向旋转一个角度(0°<>180° ), BD的延长线交 CE于 P。(1)如图②,证明:BD=CE,BD⊥CE;(2)如图③,在旋转的过程中,当AD⊥ BD时,求出 CP的长。精品字里行间精品文档成功是必须的FGHDECBA4.如图,直线 AB的同一侧作△ ABD和△ BCE都为等边三角形,连接AE、CD,二者交点为H。求证:(1)△ ABE≌△ DBC;(2)AE=DC;(3)∠ DHA=60° ;(4)△ AGB≌△ DFB;(5)△ EGB≌△ CFB;(6)连接 GF,GF∥AC;(7)连接 HB,HB平分∠ AHC。