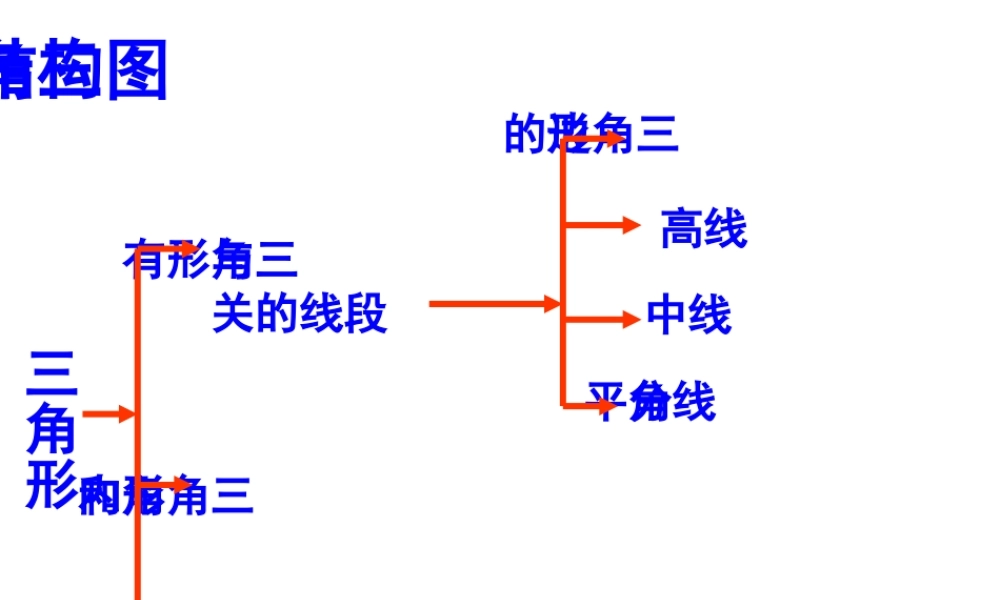
三角形与三角形有关的线段三角形内角和三角形的外角三角形知识结构图三角形的边高线中线角平分线1. 三角形的三边关系 : (1) 三角形的任何两边之和大于第三边 :(2) 三角形的任何两边之差小于第三边(3) 判断三条已知线段 a 、 b 、 c 能否组成三角形 ;当 a 最长 , 且有 b+c>a 时 , 就可构成三角形。(4) 确定三角形第三边的取值范围 :两边之差 < 第三边 < 两边之和。2. 三角形的三条高线 ( 或高线所在的直线 ) 交于一点 ,锐角三角形三条高线交于三角形内部一点 ,直角三角形三条高线交于直角顶点,钝角三角形三条高线所在的直线交于三角形外部一点。3. 三角形的三条中线交于三角形内部一点。4. 三角形的三条角平分线交于三角形内部一点。5. 三角形木架的形状不会改变 , 而四边形木架的形状会改变 . 这就是说 , 三角形具有稳定性的图形, 而四边形没有稳定性。6. 三角形的内角和: 三角形的三个内角和为 直角三角形的两个锐角互余。7. 三角形的外角: 三角形一边与另一边的延长线组成的角, 叫做三角形的外角。8. 三角形的外角和: 三角形的三个外角和为9. 三角形的一个外角等于与它不相邻的两个内角的和。10. 三角形的一个外角大于与它不相邻的任何一个内角。01800360 四边形 五边形 六边形 n 边形 图 形 过一个顶点的对角线条数 分成的三角形个数 对角线总条数 n-3n-212323425923nn 四边形 五边形 六边形 n 边形 图 形 过一个顶点的对角线条数 分成的三角形个数 内角和 外角和 n-3n-23×18004×1800 (n-2)×18001232342×18003600360036003600结论 2 :形状大小相同的任意四边形可镶嵌成一个平面123 4镶嵌条件:同一顶点处的各角和为360°结论 1 :形状大小相同的任意三角形可镶嵌 成一个平面 .原因:交点处角度之和为360° 1 、已知两条线段的长分别是 3cm 、 8cm , 要想拼成一个三角形,且第三条线段 a的 长为奇数,问第三条线段应取多少长? 知识应用 2 、等腰三角形一边的长是 5 cm ,另一边的长是 8cm ,求它的周长0. 12,34,100 ,AX 6. 已知求 的值。ABCX2314如图,计算∠ BOCABOC203051让 我 们 一 起 去 发 现2 、如图,∠ 1=27.5° ,∠ 2=95° , ∠ 3=38.5° ,则∠ 4 的大小是12341 、△ ABC 中 , 若∠ A=B+C∠∠,则△ ABC 是 三角形 .8 、如图,∠ BOC=138° ...