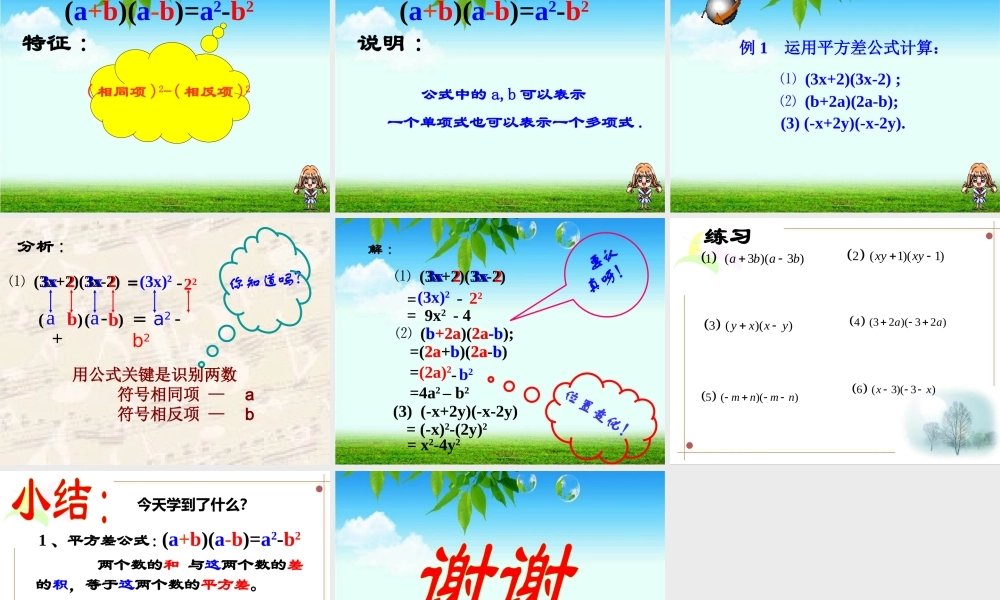
§14.2.1 平方差公式 授课人 杨巧清单位 沙栏中学(a+b)(m+n)=多项式与多项式相乘的法则:bn.知识回顾am+an+bm+ 多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加。 计算下列多项式的积 , 你能发现什么规律 ?(1) ( x+1 ) ( x-1) = = ;(2) ( m+2 )( m-2) = = ;(3)(2x+3 )( 2x-3 ) = = .x2-1m2- 44x2-9x2-x+x-1m2-m+m- 44x2-6x+6x-9 两个数的和 请认真观察上面三个式子的计算过程,你发现了什么规律?两个数的差X这两个数的平方差=(a-b) 两个数的和两个数的差X这两个数的平方差=(a+b)(a-b)= a2-ab+ab-b2-ab+ab= a2-b2a2 b2证明:(a+b) = a2-b2(a+b)(a-b)=a2-b2 两个数的和 与这两个数的差的积,等于这两个数的平方差。平方差公式: 文字表达abbab 你能根据图中的面积说明平方差公式吗?aab图 1(a+b)(a -b)a2 - b2=图 2baabbaabbabaa-b(2a+2b)(a - b) ÷2=(a+b)(a - b)=a2 - b2图 1(a+b)(a-b)=a2-b2特征 :两个数的和这两个数的差这两数的平方差(a+b)(a-b)=a2-b2特征 :两个二项式相乘(a+b)(a-b)=a2-b2特征 :相同(a+b)(a-b)=a2-b2特征 :相反(a+b)(a-b)=a2-b2特征 :平方差(a+b)(a-b)=a2-b2特征 :( 相同项 )2-( 相反项 )2(a+b)(a-b)=a2-b2说明 : 公式中的 a,b 可以表示 一个单项式也可以表示一个多项式 .例 1 运用平方差公式计算: ⑴ (3x+2)(3x-2) ; ⑵ (b+2a)(2a-b); (3) (-x+2y)(-x-2y).分析 : ⑴ (3x+2)(3x-2) 3x3xaa22bb( +)( - ) = a2 - b2=(3x)2 -22你知道吗?用公式关键是识别两数 符号相同项 — a 符号相反项 — b解 : ⑴ (3x+2)(3x-2) =(3x)23x3x-2222= 9x2 - 4 ⑵ (b+2a)(2a-b);b-b+2a 2a=(2a+b)(2a-b)2a2a=(2a)2 =4a2 – b2bb-b2 要认真呀!位置变化! (3) (-x+2y)(-x-2y) = (-x)2-(2y)2= x2-4y2 1 (3 )(3 )ab ab 2 (1)(1)xyxy 3 ()()yx xy 4 (32 )( 32 )aa 5 ()()mnmn 6 (3)( 3)xx练习1 、平方差公式:2 、利用平方差公式的关键 :(a+b)(a-b)=a2-b2识别两数 符号相同项 — a 符号相反项 — b 两个数的和 与这两个数的差的积,等于这两个数的平方差。今天学到了什么?