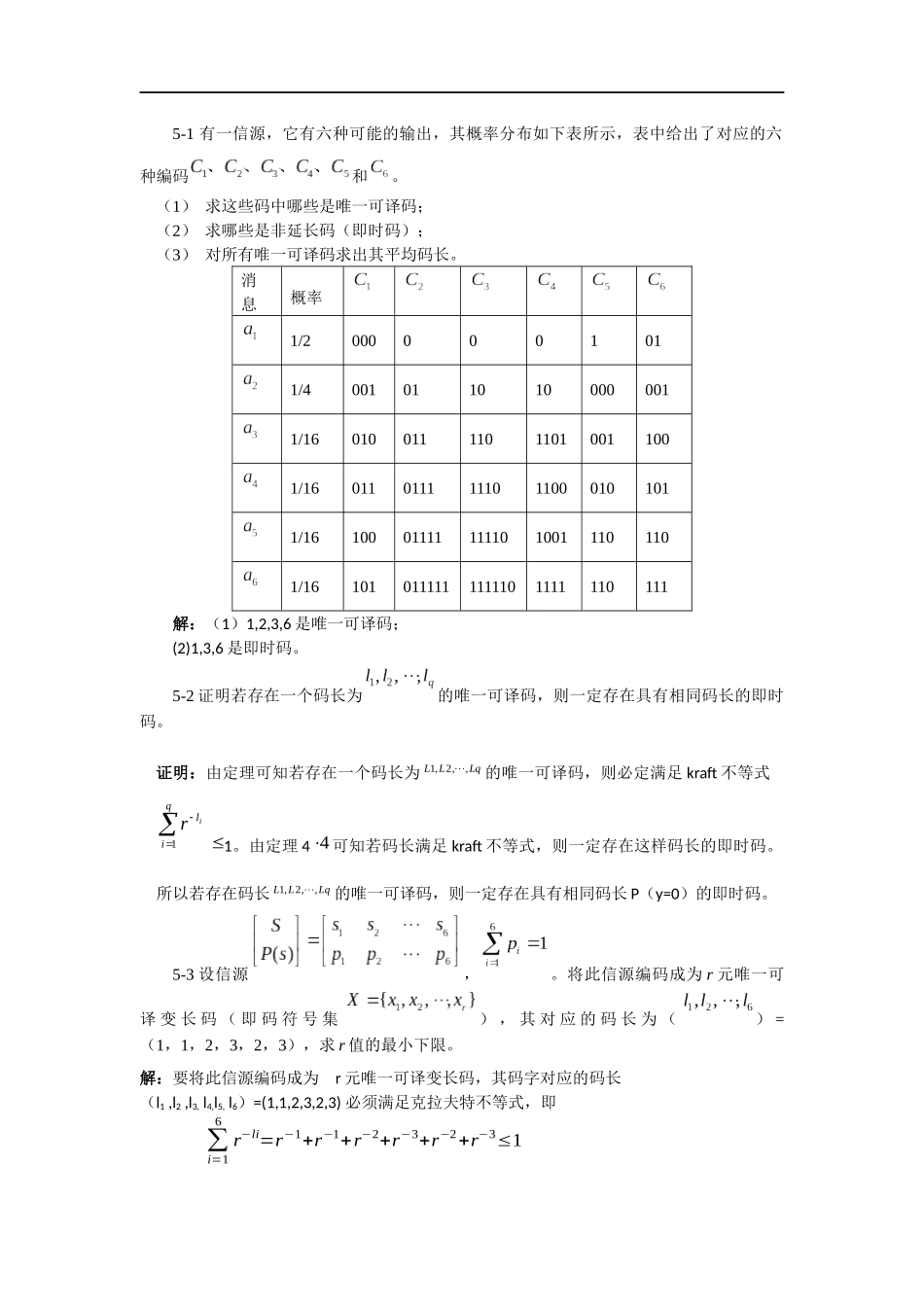
5-1有一信源,它有六种可能的输出,其概率分布如下表所示,表中给出了对应的六种编码和。(1)求这些码中哪些是唯一可译码;(2)求哪些是非延长码(即时码);(3)对所有唯一可译码求出其平均码长。消息概率1/20000001011/40010110100000011/1601001111011010011001/160110111111011000101011/16100011111111010011101101/161010111111111101111110111解:(1)1,2,3,6是唯一可译码;(2)1,3,6是即时码。5-2证明若存在一个码长为的唯一可译码,则一定存在具有相同码长的即时码。证明:由定理可知若存在一个码长为LqLL,,2,1的唯一可译码,则必定满足kraft不等式qilir11。由定理44可知若码长满足kraft不等式,则一定存在这样码长的即时码。所以若存在码长LqLL,,2,1的唯一可译码,则一定存在具有相同码长P(y=0)的即时码。5-3设信源,。将此信源编码成为r元唯一可译变长码(即码符号集),其对应的码长为()=(1,1,2,3,2,3),求r值的最小下限。解:要将此信源编码成为r元唯一可译变长码,其码字对应的码长(l1,l2,l3,l4,l5,l6)=(1,1,2,3,2,3)必须满足克拉夫特不等式,即∑i=16r−li=r−1+r−1+r−2+r−3+r−2+r−3≤1所以要满足2r+2r2+2r3≤1,其中r是大于或等于1的正整数。可见,当r=1时,不能满足Kraft不等式。当r=2,22+24+28>1,不能满足Kraft。当r=3,23+29+227=2627<1,满足Kraft。所以,求得r的最大值下限值等于3。5-4设某城市有805门公务电话和60000门居民电话。作为系统工程师,你需要为这些用户分配电话号码。所有号码均是十进制数,且不考虑电话系统中0、1不可用在号码首位的限制。(提示:用异前缀码概念)(1)如果要求所有公务电话号码为3位长,所有居民电话号码等长,求居民号码长度的最小值;(2)设城市分为A、B两个区,其中A区有9000门电话,B区有51000门电话。现进一步要求A区的电话号码比B区的短1位,试求A区号码长度的最小值。解:(a)805门电话要占用1000个3位数中的805个,即要占用首位为0~7的所有数字及以8为首的5个数字。因为要求居民电话号码等长,以9为首的数字5位长可定义10000个号码,6位长可定义100000个号码。所以。或由Craft不等式,有解得,即(b)在(a)的基础上,将80为首的数字用于最后5个公务电话,81~86为首的6位数用于B区51000个号码,以9为首的5位数用于A区9000个号码。所以,。或由Draft不等式,有或解得即5-5求概率分布为(13,15,15,215,215)的信源的二元霍夫曼码。讨论此码对于概率分布为(15,15,15,15,15)的信源也是最佳二元码。解:信源的概率分布为:p(si)=(13,15,15,215,215)二元霍夫曼码:00,10,11,010,011,码长:2,2,2,3,3当信源给定时,二元霍夫曼码是最佳二元码。所以对于概率分布为(15,15,15,15,15)的信源,其最佳二元码就是二元霍夫曼码。这二元霍夫曼码一定是三个信源符号的码长为2(码符号/信源符号),另二个信源符号的码长为3(码符号/信源符号),其平均码长最短。因此,上述对概率分布为(13,15,15,215,215)信源所编的二元霍夫曼码也是概略分布为(15,15,15,15,15)信源的最佳二元码。5-6设二元霍夫曼码为(00,01,10,11)和(0,10,110,111),求出可以编得这些霍夫曼码的信源的所有概率分布。解:由题意假设信源所发出的是个符号的概率为P(S4)≥P(S3)≥P(S2)≥P(S1)由霍夫曼编码的特点知:P(S4)+P(S3)+P(S2)+P(S1)=1根据霍夫曼编码的方法,每次概率最小的两个信源符号合并成一个符号,构成新的缩减信源,直至最后只剩两个符号。而且当缩减信源中的所有符号概率相等时,总是将合并的符号放在最上面。所以,对于二元霍夫曼码为(00,01,10,11)来说,每个信源都要缩减一次,所以要大于和,这时必有同理对于二元霍夫曼码为(0,10,110,111)有信源概率分布满足以上条件则其霍夫曼编码符合题意。5-7设一信源有K=6个符号,其概率分别为:,,,对该信源进行霍夫曼二进制编码,并求编码效率。解:相应的Huffman编码是:{1,01,001,0001,00000,00001}。平均码长=1.95,熵=1.945-8设信源概率空间为:[SP(s)]=[s1,s20.1,0.9],(1)求H(S)和信源冗余度;(2)设码符号为X={0,1},编出S的紧致码,...