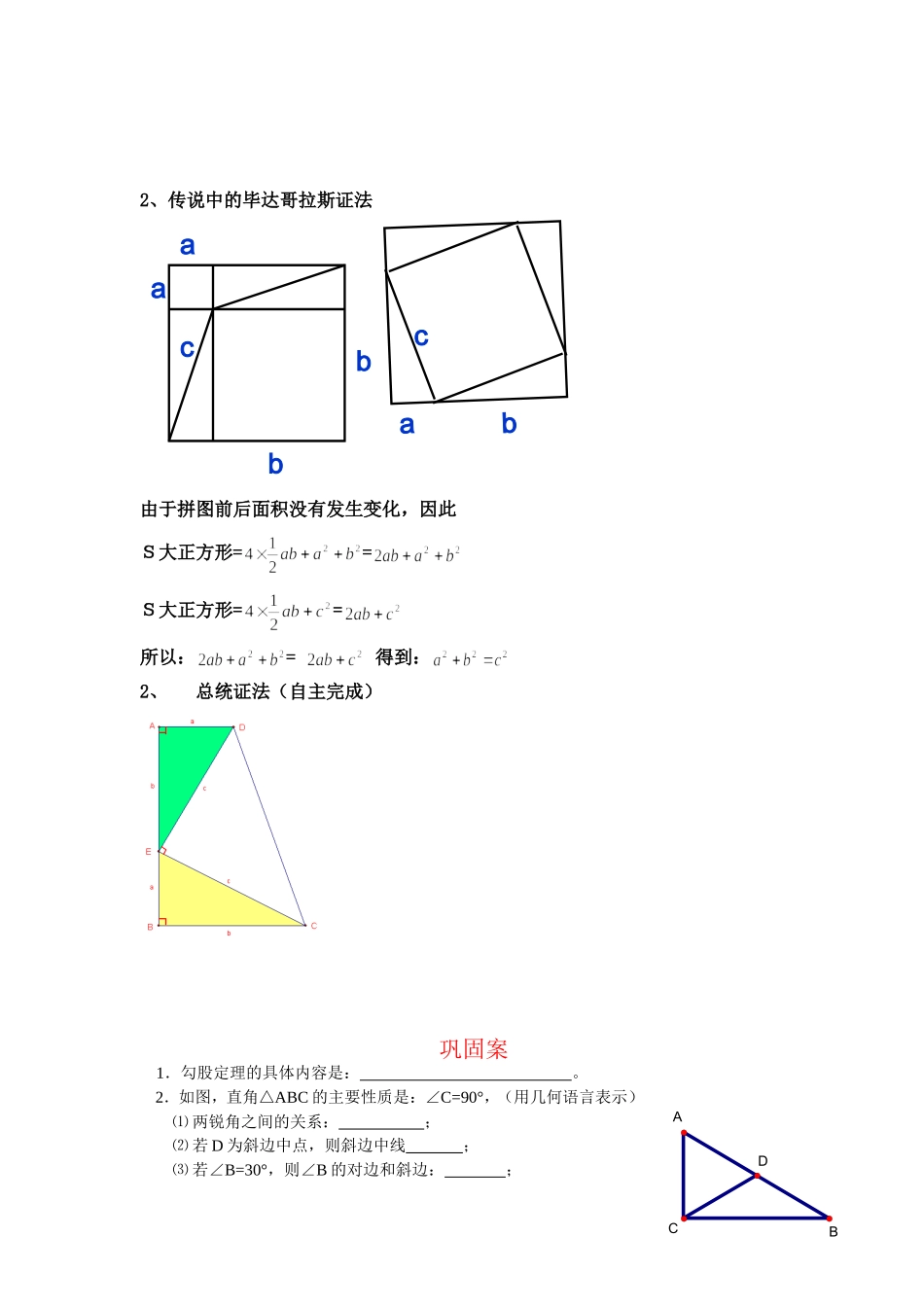
勾股定理 (第一课时)教学目标:1、理解并掌握勾股定理的证明;并且能初步运用勾股定理解决问题。2、在探索过程中,让学生亲历“观察—猜想—归纳—证明”的过程,并且能体会特殊到一般、数形结合的数学思想和方法。3、通过了解与定理有关的中外数学史,激发学生的学习兴趣和研究精神。特别是通过了解中国古代的数学成就,激发学生的民族自豪感。 教学重点:勾股定理的证明和运用 教学难点:勾股定理的证明教 案(一)合作交流,探究新知早在 2500 年前,古希腊数学家毕达哥拉斯从朋友家的地砖铺成的地面上找到了灵感,并且对此展开研究,下面我们也来重温数学家的发现之路,探究这个“饭局中诞生的定理”。活动一 探究:等腰直角三角形三边的关系思考:(1)你能发现图中的三个正方形的面积之间有什么联系吗?(2)、你能用直角三角形的边长表示正方形的面积吗?(3)、你能发现图中的直角三角形三边长度之间存在什么关系吗?初步猜想:在等腰直角三角形中,两直角边的平方和等于斜边的平方。cabcabcabcab活动二 探究:一般直角三角形三边之间的关系是否也是如此?(1)图形 A 的面积= ,图形 B 的面积= 交流:图形 C 的面积如何求出?(2)、你能用直角三角形的边长表示正方形的面积吗?(3)、你能发现图中的直角三角形三边长度之间存在什么关系吗?进一步猜想:在直角三角形中,两直角边的平方和等于斜边的平方。以上仅仅是我们的猜想,这个命题如何来进行证明呢?得到勾股定理在直角三角形中,两直角边的平方和等于斜边的平方。 学案我国古代人民早在几千万年以前就已经发现和运用勾股定理,在已有的文献记载中,最早给出证明的是三国时期的吴国数学家赵爽在《周髀算经》注中已经给出了勾股定理的证明。指导学生利用手中 4 个全等的直角三角形进行拼图。1、赵爽“勾股圆方图” 大正方形的面积可以表示为 也可以表示为 4×+,于是可得:=4×+ 整理的:得到勾股定理在直角三角形中,两直角边的平方和等于斜边的平方。 A B C 2、传说中的毕达哥拉斯证法由于拼图前后面积没有发生变化,因此S大正方形==S大正方形==所以:= 得到:2、总统证法(自主完成)巩固案1.勾股定理的具体内容是: 。2.如图,直角△ABC 的主要性质是:∠C=90°,(用几何语言表示)⑴ 两锐角之间的关系: ;⑵ 若 D 为斜边中点,则斜边中线 ;⑶ 若∠B=30°,则∠B 的对边和斜边: ;acabbabcACBD⑷ 三边之间的关系: 。3、一个长...