高中数学 椭圆的定义与标准方程(1) 新人教A版选修1-1 课件VIP免费

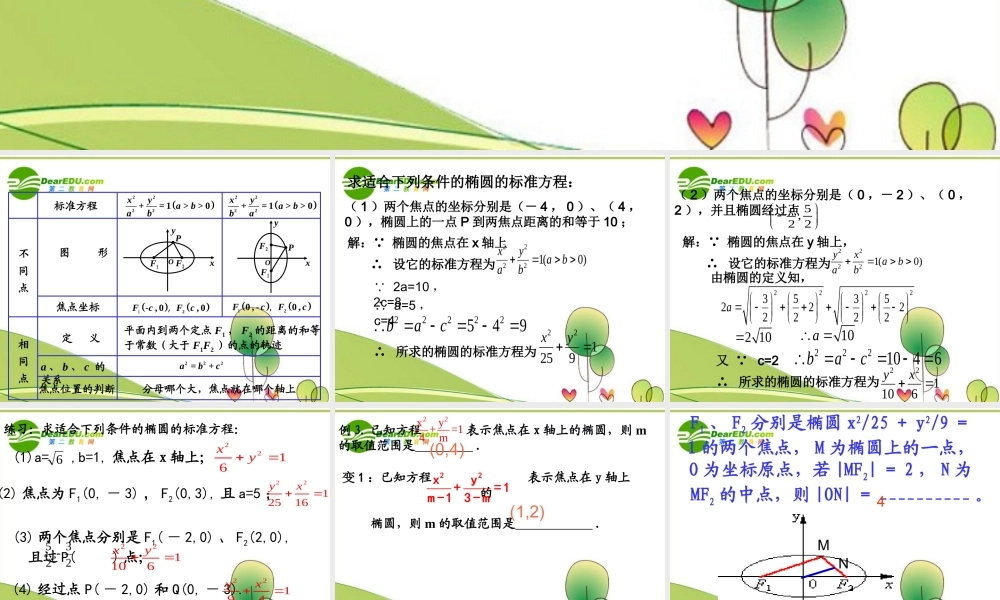
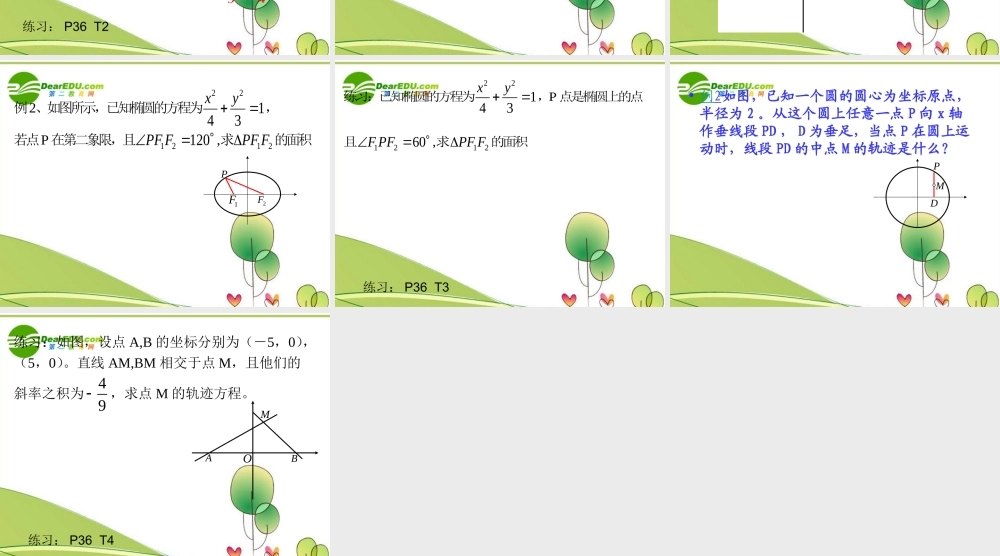
2222+= 1 >> 0xyabab2222+= 1 >> 0xyabba分母哪个大，焦点就在哪个轴上222=+abc平面内到两个定点 F1 ， F2 的距离的和等于常数（大于 F1F2 ）的点的轨迹12- , 0 , 0，FcFc120 , -0 ,，FcFc标准方程不 同 点相 同 点图 形焦点坐标定 义a 、 b 、 c 的关系焦点位置的判断xyF1F2POxyF1F2PO求适合下列条件的椭圆的标准方程：（ 1 ）两个焦点的坐标分别是（－ 4 ， 0 ）、（ 4 ，0 ），椭圆上的一点 P 到两焦点距离的和等于 10 ；解：∵ 椭圆的焦点在 x 轴上∴ 设它的标准方程为∴ 所求的椭圆的标准方程为22221(0)xyabab  ∵ 2a=10 ， 2c=8 ∴ a=5 ， c=422222549bac221259xy（ 2 ）两个焦点的坐标分别是（ 0 ，－ 2 ）、（ 0 ，2 ），并且椭圆经过点解：∵ 椭圆的焦点在 y 轴上，由椭圆的定义知，3 5,2 2∴ 设它的标准方程为22221(0)yxabab222235352222222a2 1010a 又 ∵ c=222210 46bac∴ 所求的椭圆的标准方程为221106yx练习：求适合下列条件的椭圆的标准方程：(2) 焦点为 F1(0, － 3) ， F2(0,3), 且 a=5 ；2212516yx2216xy(1)a= ,b=1, 焦点在 x 轴上；(3) 两个焦点分别是 F1( － 2,0) 、 F2(2,0),且过 P( ) 点； (4) 经过点 P( － 2,0) 和 Q(0, － 3).622194yx23,25 221106xy练习： P36 T2例 3. 已知方程 表示焦点在 x 轴上的椭圆，则 m的取值范围是 .22xy+=14m(0,4) 变 1 ：已知方程 表示焦点在 y 轴上的 椭圆，则 m 的取值范围是 .22xy+= 1m -13 - m(1,2)F1 、 F2 分别是椭圆 x2/25 ＋ y2/9 ＝1 的两个焦点， M 为椭圆上的一点，O 为坐标原点，若 |MF2| ＝ 2 ， N 为MF2 的中点，则 |ON| ＝ __________ 。 MN4例2、如图所示，已知椭圆的方程为22143xy ， 若点P 在第二象限，且12120PF F ,求12PF F的面积 P1F2F练习：已知椭圆的方程为22143xy ，P 点是椭圆上的点 且1260F PF ,求12PF F的面积 练习： P36 T3• 例2如图，已知一个圆的圆心为坐标原点，半径为 2 。从这个圆上任意一点 P 向 x 轴作垂线段 PD ， D 为垂足，当点 P 在圆上运动时，线段 PD 的中点 M 的轨迹是什么？PDM练习：如图，设点 A,B 的坐标分别为（－5，0）， （5，0）。直线 AM,BM 相交于点 M，且他们的 斜率之积为49，求点 M 的轨迹方程。 ABMO练习： P36 T4