高中数学 3.2立体几何中的向量方法(第3课时)课件 新人教A版选修2 1 课件VIP免费

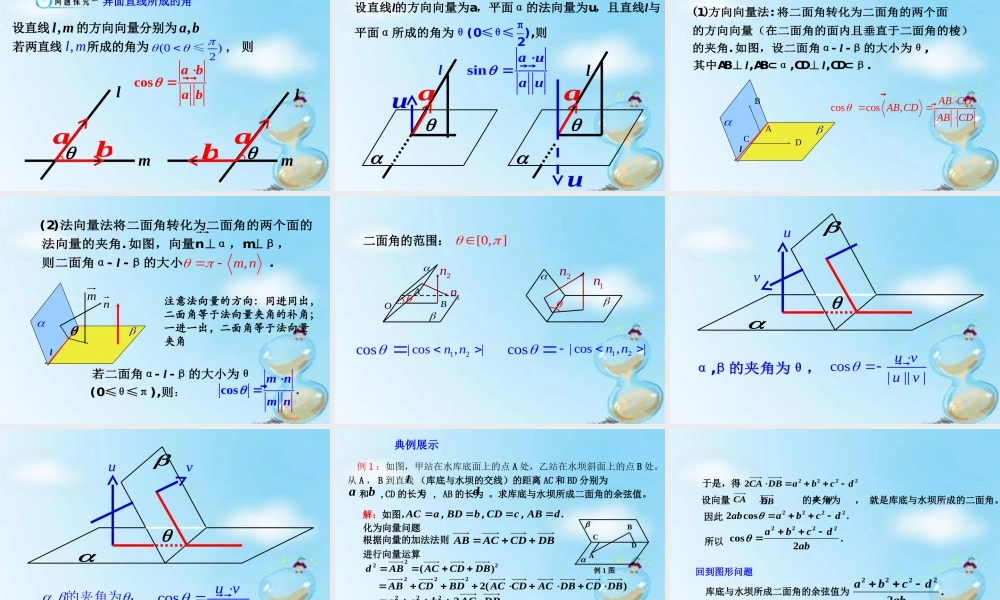
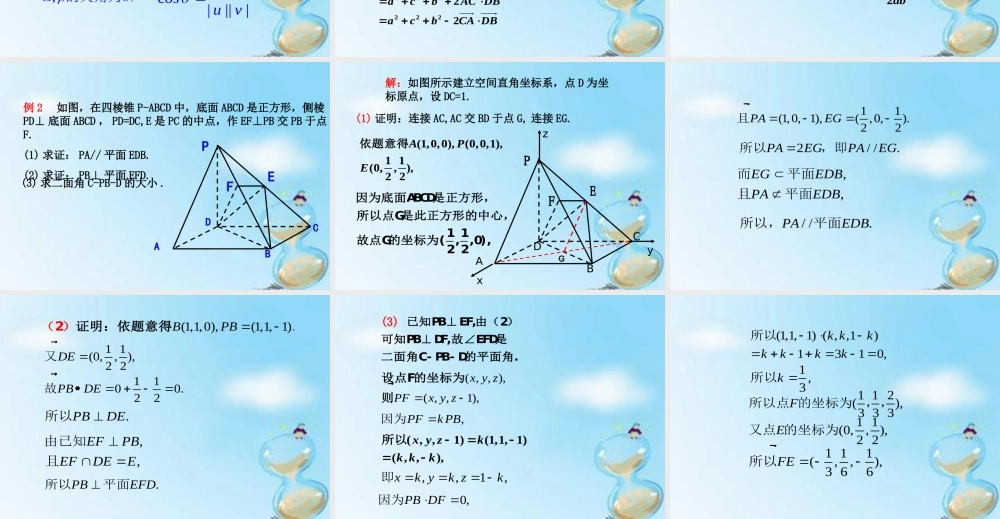
3.2 立体几何中的向量法 (3)第三章 空间向量与立体几何—— 空间向量与空间角本节课主要学习利用空间向量求异面直线所成的角、直线与平面所成的角、二面角 . 以学生探究为主，探讨如何利用空间向量求异面直线所成的角、直线与平面所成的角、二面角等 . 讲解二面角的平面角与两个半平面的法向量之间的关系，突破难点。通过例 1 和例 2 巩固掌握二面角的求法，证明线面平行，线面垂直的方法。例 3 是证明线面平行及求异面直线所成的角，本题可以作为一道备用题，如果时间不许可，可以直接点击链接“课堂检测”，进入课堂检测部分。运用转化思想，将立体几何中的线线角、线面角、二面角转化为空间向量所成的角，再用数量积的定义求相应的角。http://www.jtyhjy.com/edu/ppt/ppt_playVideo.action?mediaVo.resId=54260de45aa8a9cc1dd7292f动画展示面与面的夹角 空间向量的引入为代数方法处理立体几何问题提供了一种重要的工具和方法，解题时，可用定量的计算代替定性的分析，从而避免了一些繁琐的推理论证 . 求空间角与距离是立体几何的一类重要的问题，也是高考的热点之一 . 本节课主要是讨论怎样用向量的办法解决空间角问题 .用空间向量解决立体几何问题的三步曲：1. （化为向量问题）建立立体图形与空间向量的联系，用空间向量表示问题中涉及的点、直线、平面，把立体几何问题转化为向量问题 .2. （进行向量运算）通过向量运算，研究点、直线、平面之间的位置关系以及它们之间距离和夹角等问题 .3. （回到图形问题）把向量的运算结果“翻译”成相应的几何意义 .OABaabb两个向量的夹角 如图,已知两个非零向量 ,a b,在空间任取一点O ,作OAa�, OBb�,则AOB叫做向量 a与b的夹角,记作:,a b. ⑴范围:0,a b≤≤. ⑵,,＝a bb a. ⑶如果,2a b ,则称 a与 b垂直,记为 ab .两个向量的夹角 已知空间两个非零向量 ,a b,则,a b 叫做 ,a b的夹角. 即 cos,a ba ba b . 异面直线所成的角设直线 ,l m 的方向向量分别为 ,a b lamlamb若两直线 所成的角为 , 则,l m(0)2≤cosa ba bb线面角u aulasina ua u设直线 的方向向量为a，平面α的法向量为u，且直线 与平面α所成的角为π0≤θ,θ则...