高三数学高考专题十一 空间向量及其应用 试题VIP免费

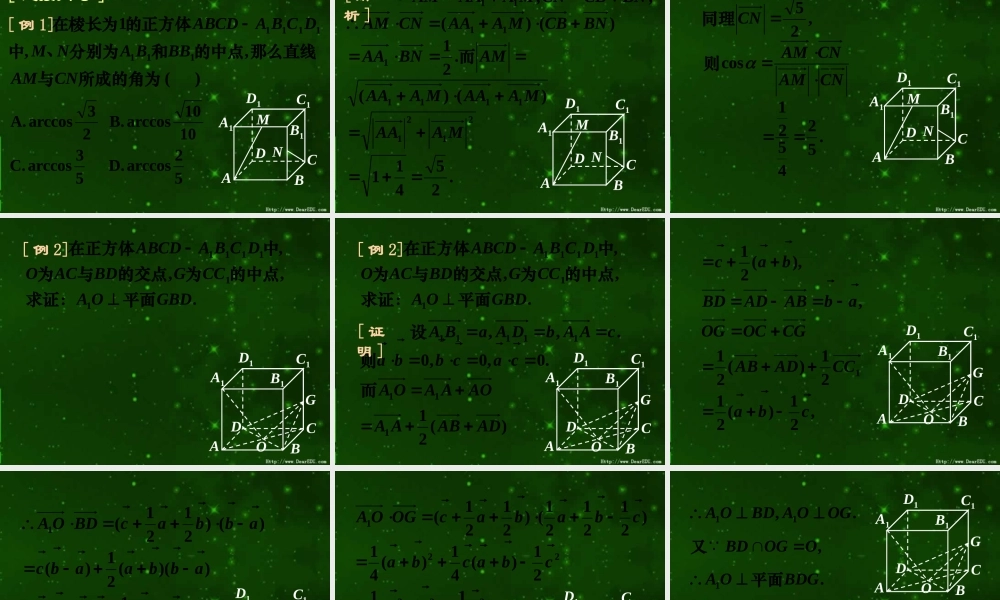
空间向量及应用第一课时：空间向量及其运算[ 课前导引 ]第一课时：空间向量及其运算第一课时：空间向量及其运算[ 课前导引 ] 1. 平行四面体 ABCD-A1B1C1D1 中 , M为 AC 和 BD 的交点 , 若 AAbDAaBA11111,,) ( ,1相等的是则下列式子中与MBccba2121 A.cba 2121 B.cba 2121 C.cba2121 D.[ 解析 ] 如图 ,BMBBMB11.21212121)(21111111cacDABAAABCBABBABB1MCDC1A1D1[ 解析 ] 如图 ,答案： ABMBBMB11.21212121)(21111111cacDABAAABCBABBABB1MCDC1A1D1 2. P 是二面角 -AB- 棱上的一点 , 分别在、 平面上引射线 PM 、 PN, 如果∠ MPN=60, 那么二面角 -AB- 的大小为 ( ) A. 30 B. 60 C. 90 D. 120ABFENPM 2. P 是二面角 -AB- 棱上的一点 , 分别在、 平面上引射线 PM 、 PN, 如果∠ MPN=60, 那么二面角 -AB- 的大小为 ( ) A. 30 B. 60 C. 90 D. 120[ 解析 ] 如图 , 设 PM=a, PN=b, 作ME⊥AB,∠EPM=∠EPN=45,ABFENPM,22,22bPFaPE故ABFENPM.90.0222245cos2245cos2260cos)()(即二面角为于是NFEMbabbaabPFPEPNPEPFPMPNPMPFPNPEPMFNEMABFENPM.90.0222245cos2245cos2260cos)()(即二面角为于是NFEMbabbaabPFPEPNPEPFPMPNPMPFPNPEPMFNEM答案： C[ 考点搜索 ][ 考点搜索 ] 1. 空间向量的概念，表示及其运算 . 2. 空间向量的基本定理，以及空间向量的数量积的定义和性质 . 3. 利用向量解决有关平行、垂直问题 . 4. 利用向量求空间角 . 5. 利用向量求空间距离 .[ 链接高考 ][ 链接高考 ]) ( , ,1 1111111所成的角为与那么直线的中点和分别为、中的正方体在棱长为CNAMBBBANMDCBAABCD [ 例 1]52arccos D. 53arccos C.1010arccos B. 23arccos A.A1B1C1D1ABDCNM.25411)()(.21)()(,, 2121111111111MAAAMAAAMAAAAMBNAABNCBMAAACNAMBNCBCNMAAAAM而[ 解析 ]A1B1C1D1ABDCNM.524521 cos,25CNAMCNAMCN则同理A1B1C1D1ABDCNM.,,, 111111GBDOACCGBDACODCBAABCD平面求...