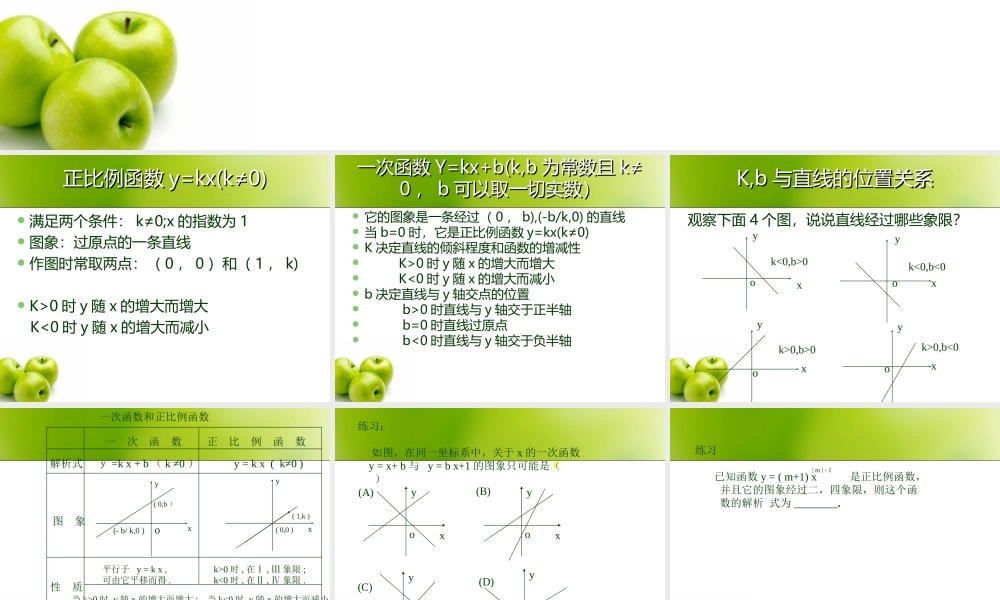
正比例函数正比例函数 y=kx(k≠0)y=kx(k≠0) 满足两个条件: k≠0;x 的指数为 1 图象:过原点的一条直线 作图时常取两点:( 0 , 0 )和( 1 , k) K>0 时 y 随 x 的增大而增大 K<0 时 y 随 x 的增大而减小一次函数一次函数 Y=kx+b(k,bY=kx+b(k,b 为常数且为常数且 k≠k≠00 ,, bb 可以取一切实数)可以取一切实数) 它的图象是一条经过( 0 , b),(-b/k,0) 的直线 当 b=0 时,它是正比例函数 y=kx(k≠0) K 决定直线的倾斜程度和函数的增减性 K>0 时 y 随 x 的增大而增大 K<0 时 y 随 x 的增大而减小 b 决定直线与 y 轴交点的位置 b>0 时直线与 y 轴交于正半轴 b=0 时直线过原点 b<0 时直线与 y 轴交于负半轴K,bK,b 与直线的位置关系与直线的位置关系观察下面 4 个图,说说直线经过哪些象限?xyoyxoyxoyxok<0,b>0k<0,b<0k>0,b>0k>0,b<0一次函数和正比例函数 一 次 函 数正 比 例 函 数解析式y =k x + b ( k ≠0 ) y = k x ( k≠0 ) 图 象xy( 0,b )(- b/ k,0 )oyx( 0,0 )( 1,k )性 质平行于 y = k x ,可由它平移而得 . k>0 时 , 在Ⅰ , Ⅲ 象限 ;k<0 时 , 在Ⅱ , Ⅳ 象限 .当 k>0 时 ,y 随 x 的增大而增大 ; 当 k<0 时 ,y 随 x 的增大而减小 .应 用(1). 待定系数法 ;(2). 解决方程 , 不等式 , 方程组的有关问题 .练习: 如图,在同一坐标系中,关于 x 的一次函数 y = x+ b 与 y = b x+1 的图象只可能是( )xyoxyoxyoxyo(A)(B)(C)(D)C练习 已知函数 y = ( m+1) x 是正比例函数, 并且它的图象经过二,四象限,则这个函 数的解析 式为 ________.| m | - 1练习: 如果一次函数 y=kx+b 的图象经过第一、三、四象限,则 k _ 0 , b _ 0练习练习 直线 y=kx+3 与两坐标轴围成三角形的面积为 9 ,求 k 的值。基础准备:1 、形如 __________ 的函数是正比例函数,它的图象是一条 ___________ ,当 k>0 时, y 随 x 的增大而 ____, 且图象经过第 _____象限;当 k<0 时, y 随 x 的增大而 ____ ,且图象经过第 _____ 象限。2 、形如 _____________ 的函数是一次函数,它的图象是一条 ____ ,此图象与 x 轴的交点坐标为 _________ ,与 y 轴的交点坐标为______ 。所以 ,...