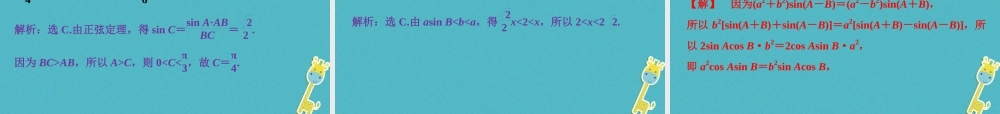1.1 正弦定理和余弦定理 1.1.1 正弦定理 第一章 解三角形 1.通过对任意三角形边长和角度关系的探索,掌握正弦定理的内容及其证明方法. 2.能运用正弦定理与三角形内角和定理解决简单的解三角形问题. 第一章 解三角形 1.正弦定理 条件 在△ABC 中,角 A,B,C 所对的边分别为 a,b,c 结论 ________=bsin B=_______ 文字 叙述 在一个三角形中,各边和它所对角的_____的比相等 asin A csin C 正弦2.三角形的元素与解三角形 (1)三角形的元素 把三角形的_________________和它们的______________叫做三角形的元素. (2)解三角形 已知三角形的___________求其他______的过程叫做解三角形. 三个角 A , B , C几个元素元素对边 a , b ,c 1.对正弦定理的理解 (1)适用范围:正弦定理对任意的三角形都成立. (2)结构形式:分子为三角形的边长,分母为相应边所对角的正弦的连等式. (3)揭示规律:正弦定理指出的是三角形中三条边与其对应角的正弦之间的一个关系式,它描述了三角形中边与角的一种数量关系. (4)主要功能:正弦定理的主要功能是实现三角形中边角关系的转化. 2.正弦定理的变形公式 判断正误(正确的打“√”,错误的打“×”) (1)正弦定理不适用于直角三角形.( ) (2)在△ABC 中必有 asin A=bsin B.( ) (3)在△ABC 中,若 A>B,则必有 sin A>sin B.( ) (4)在△ABC 中,若 sin A>sin B,则必有 A>B.( ) (5)在△ABC 中,若 A>B,则必有 cos A>cos B.( ) 答案:(1)× (2)× (3)√ (4)√ (5)× 在△ABC 中,若角 A,B,C 的对边分别是 a,b,c,则下列各式一定成立的是( ) A.ab=cos Acos B B.ab=sin Asin B C.asin B=bcos A D.acos B=bsin A 解析:选 B.在△ABC 中,由正弦定理asin A=bsin B,得ab=sin Asin B. 在△ABC 中,a=3,b=5,sin A=13,则 sin B=( ) A.15 B.59 C. 53 D.1 解析:选 B.因为 a=3,b=5,sin A=13,所以由正弦定理得 sin B=bsin Aa=5×133 =59. 在△ABC 中,若 A=60°,B=45°,BC=3 2,则 AC 的长为________. 解 析 : 如 图 , 由 正 弦 定 理 得|AC|sin 45° =3 2sin 60°,即|AC|=3 2sin 45°sin 60°= 332=2 3. 答案:2 3 在△ABC 中,若sin Aa=cos Bb,则 B 的值为________. 解析:根据正弦定...