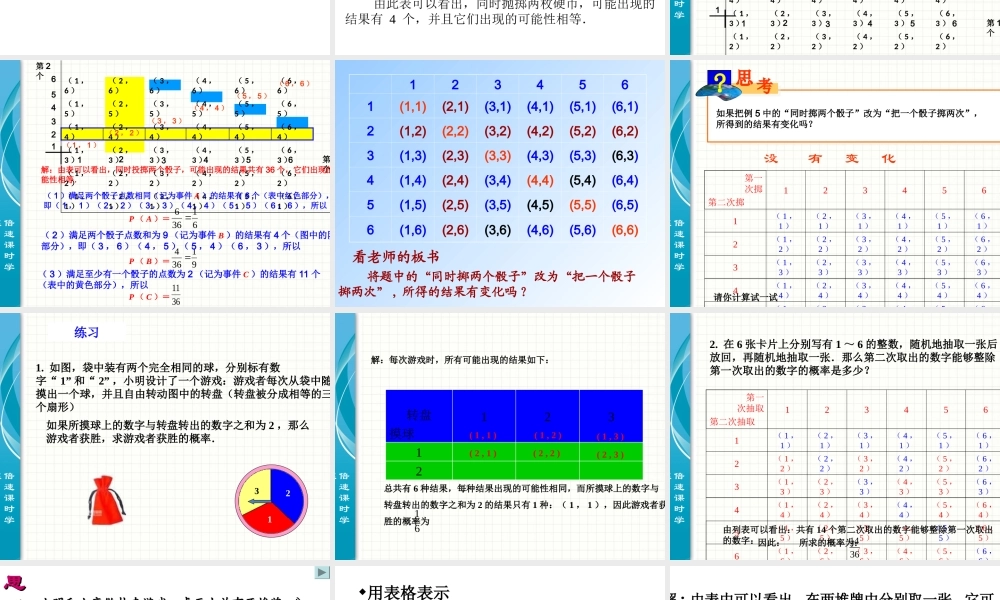
在一次试验中,如果可能出现的结果只有有限个,且各种结果出现的可能性大小相等,那么我们可以通过列举试验结果的方法,求出随机事件发生的概率,这种求概率的方法叫列举法. 1 .复习旧知 例 1 同时向空中抛掷两枚质地均匀的硬币,求下列事件的概率: ( 1 )两枚硬币全部正面向上; ( 2 )两枚硬币全部反面向上; ( 3 )一枚硬币正面向上、一枚硬币反面向上.2 .探究新知 方法一:将两枚硬币分别记做 A 、 B ,于是可以直接列举得到:( A 正, B 正),( A 正, B 反), ( A 反, B 正), ( A 反, B 反)四种等可能的结果.故:2 .探究新知 P (两枚正面向上) = .41 P (两枚反面向上) = .41 P (一枚正面向上,一枚反面向上) = .21 方法二:将同时掷两枚硬币,想象为先掷一枚,再掷一枚,分步思考:在第一枚为正面的情况下第二枚硬币有正、反两种情况,同理第一枚为反面的情况下第二枚硬币有正、反两种情况.2 .探究新知 两枚硬币分别记为第 1 枚和第 2 枚,可以用下表列举出所有可能出现的结果. 正反正(正,正) (反,正)反(正,反) (反,反)第 1 枚第 2 枚 由此表可以看出,同时抛掷两枚硬币,可能出现的 结果有 4 个,并且它们出现的可能性相等.2 .探究新知 列表法倍速课时学练 例 5 同时掷两个质地均匀的骰子,计算下列事件的概率: ( 1 )两个骰子的点数相同; ( 2 )两个骰子点数的和是 9 ; ( 3 )至少有一个骰子的点数为 2.分析:当一次试验要涉及两个因素(例如掷两个骰子)并且可能出现的结果数目比较多时,为不重不漏地列出所有可能的结果,通常采用列表法,我们不妨把两个骰子分别记为第 1 个和第 2 个,这样就可以用下面的方形表格列举出所有可能出现的结果.( 1 ,6 )( 2 ,6 )( 3 ,6 )( 4 ,6 )( 5 ,6 )( 6 ,6 )( 1 ,5 )( 2 ,5 )( 3 ,5 )( 4 ,5 )( 5 ,5 )( 6 ,5 )( 1 ,4 )( 2 ,4 )( 3 ,4 )( 4 ,4 )( 5 ,4 )( 6 ,4 )( 1 ,3 )( 2 ,3 )( 3 ,3 )( 4 ,3 )( 5 ,3 )( 6 ,3 )( 1 ,2 )( 2 ,2 )( 3 ,2 )( 4 ,2 )( 5 ,2 )( 6 ,2 )( 1 ,1 )( 2 ,1 )( 3 ,1 )( 4 ,1 )( 5 ,1 )( 6 ,1 )...