高中数学 直接证明课件 苏教版选修2-2 课件VIP免费

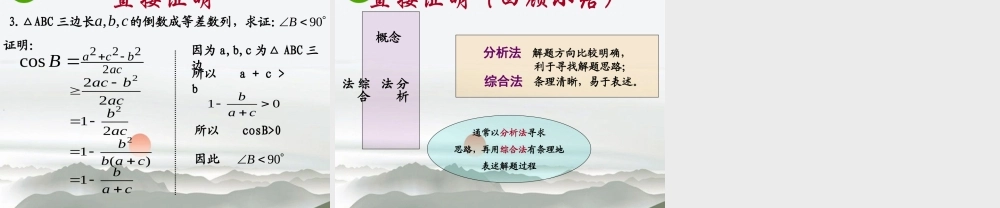
2.2.1 直接证明引例 1:已知 : 四边形是 ABCD 平行四边形 .求证 :AB=CD,BC=DA2134证明 : 连结 AC, 四边形ABCD 是平行四边形 ∴AB∥CD,BC∥CD故∠ 1=∠2, ∠3=∠4又 AC=CA ∴⊿ABC≌⊿CDA∴AB=CD,BC=DAABCD直接从原命题的条件逐步推得命题成立 , 这种证法通常称为直接证明 .直接证明的一般形式 :ABC …本题结论已知定义本题条件已知公理已知定理引例 2 ：回顾基本不等式： (a>0,b>0) 的证明 .a + bab2证明 :因为 : 所以所以所以 成立()b20a20a + bab2a + baba + bab2证明 : 要证只需证 :只需证 :只需证 :因为 : 成立所以 成立a + bab22a + bab20a + bab()b20a()b20aa + bab2利用已知条件和某些数学定义、公理、定理等 , 经过一系列的推理论证 , 最后推导出所要证明的结论成立 , 这种证明方法叫做综合法用 P 表示已知条件、已有的定义、公理、定理等 ,Q 表示所要证明的结论 .则综合法用框图表示为 :1PQ12QQ23QQnQQ…综合法推证过程 :已知条件结论……由因导果 一般地，从要证明的结论出发，逐步寻求推证过程中，使每一步结论成立的充分条件，直至最后，把要证明的结论归结为判定一个明显成立的条件（已知条件、定理、定义、公理等）为止，这种证明的方法叫做分析法． 特点：由果索因 . 已知条件结论……分析法推证过程 :用框图表示分析法的思考过程、特点 .1QP23PP12PP得到一个明显成立的结论…直接证明（数学理论）上述两种证法有什么异同？都是直接证明证法 1 从已知条件出发，以已知的定义、公理、定理为依据，逐步下推，直到推出要证明的结论为止 综合法相同不同 证法 2 从问题的结论出发，追溯导致结论成立的条件，逐步上溯，直到使结论成立的条件和已知条件吻合为止 分析法直接证明（例题）.1DFCEBFAEBDOACOOCDAB，求证：，，交于点，如图，已知例直接证明证 （综合法） 因为BDOACO因为所以又因为所以BOAODOCO（已知）BFAE FOEO （对顶角相等）FODEOC所以FODEOC所以FDEC 直接证明证 （分析法）要证明 CE=DF ，只需证明为此只需证明FODEOCFOEOFODEOCDOCO为了证明 只需 为了证明 只需证明 也只需 DOCO BDOACOFOEO ）（因为已知BFAEBOAO（已知）BDOACO因为 是对顶角，所以它们相等，...