高中数学 3.1两角差的余弦公式课件 新人教版必修4 课件VIP免费

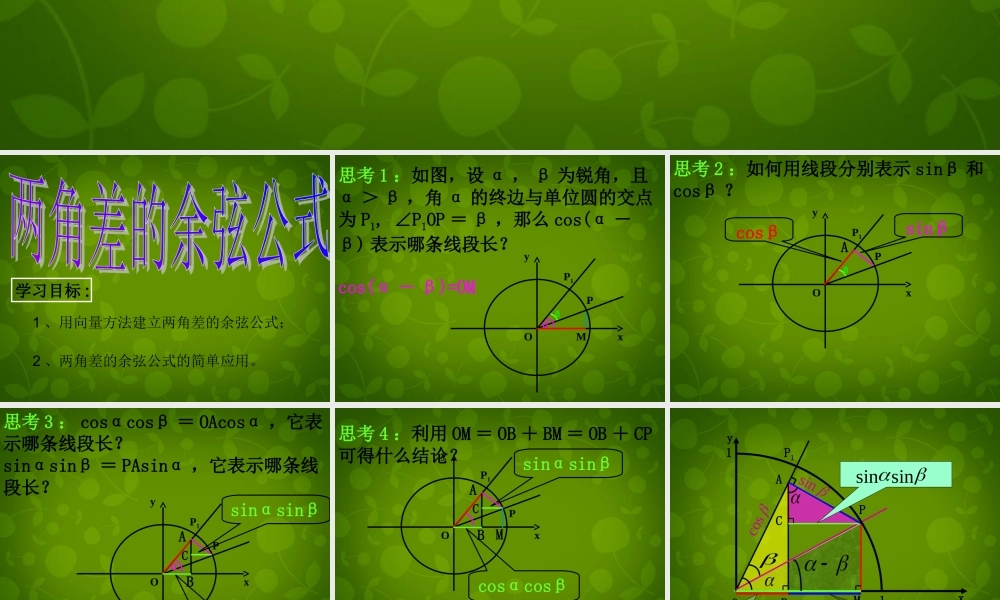
我们学习了同一个角的三角函数的性质以及各三角函数之间的相互关系． 在研究三角函数时，我们经常遇到这样的问题：已知任意角 α ， β 的三角函数值，如何求出α+β ， α-β 或 2α 的三角函数值 ? 学习目标 :1 、用向量方法建立两角差的余弦公式；2 、两角差的余弦公式的简单应用。 思考 1 ：如图，设 α ， β 为锐角，且α ＞ β ，角 α 的终边与单位圆的交点为 P1, ∠P1OP ＝ β ，那么 cos(α －β) 表示哪条线段长？MPP1Oxycos(α － β)=OMβα思考 2 ：如何用线段分别表示 sinβ 和cosβ ？PP1OxyAsinβcosββ思考 3 ： cosαcosβ ＝ OAcosα ，它表示哪条线段长？sinαsinβ ＝ PAsinα ，它表示哪条线段长？PP1OxyAsinαsinβcosαcosβBCα思考 4 ：利用 OM ＝ OB ＋ BM ＝ OB ＋ CP可得什么结论？sinαsinβcosαcosβPP1OxyABCMcos(α － β) ＝ cosαcosβ ＋ sinαsinβxyPP1MBOAC sincos+11 coscos sinsinsinsin思考 5 ：上述推理能说明对任意角 α ， β ，都有 cos(α －β) ＝ cosαcosβ ＋ sinαsinβ 成立吗？思考 6 ：如图，设角 α ， β 的终边与单位圆的交点分别为 A 、 B ，则向量 、 的坐标分别是什么？其数量积是什么？ΟΑΟBBOAxyαβ=(cosβ,sinβ)OB=(cosα,sinα)OAcosαcosβ ＋ sinαsinβOA · OBα ＝ 2kπ ＋ β ＋θ 或 β ＝ 2kπ ＋α ＋ θ BOAxyαβθcos(α － β) ＝ cosαcosβ ＋ sinαsinβ思考 7 ：向量的夹角 θ 与 α 、 β 有什么关系？根据数量积定义， 等于什么？由此可得什么结论？ OBOA ·思考 8 ：公式 cos(α － β) ＝ cosαcosβ ＋ sinαsinβ 称为差角的余弦公式，记作 ，该公式有什么特点？ C√6 + √2 4=例 1 ：利用差角余弦公式求 的值cos15分析 :cos15cos 4530解： cos15°=cos （ 45°-30°)= cos45°cos30°+sin45°sin30° √2 √3 √2 1 2 2 2 2 =+练习 1 、已知 π2cos,π3α=-α5求 的值 .πcos 4α解 :π2cos,π3=-5 ∴24sin1cos5=πππcos()coscossinsin444-+224225 35210练习 2 ：求值（ 1 ）（ 2 ）（ 3 ）探究（二）：...