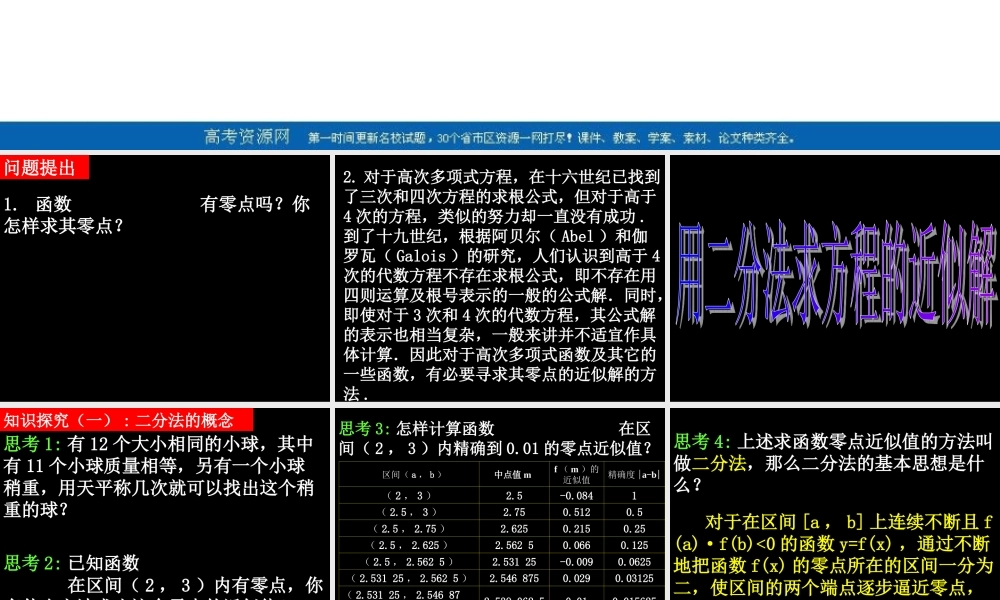
3.1.2 用二分法求方程的近似解 问题提出1. 函数 有零点吗?你怎样求其零点?34xx)x(f2 2. 对于高次多项式方程,在十六世纪已找到了三次和四次方程的求根公式,但对于高于4 次的方程,类似的努力却一直没有成功 . 到了十九世纪,根据阿贝尔( Abel )和伽罗瓦( Galois )的研究,人们认识到高于 4次的代数方程不存在求根公式,即不存在用四则运算及根号表示的一般的公式解.同时,即使对于 3 次和 4 次的代数方程,其公式解的表示也相当复杂,一般来讲并不适宜作具体计算.因此对于高次多项式函数及其它的一些函数,有必要寻求其零点的近似解的方法 . 知识探究(一) : 二分法的概念 思考 1: 有 12 个大小相同的小球,其中有 11 个小球质量相等,另有一个小球稍重,用天平称几次就可以找出这个稍重的球? 思考 2: 已知函数 在区间( 2 , 3 )内有零点,你有什么方法求出这个零点的近似值? 62xlnx)x(f 思考 3: 怎样计算函数 在区间( 2 , 3 )内精确到 0.01 的零点近似值? 62xlnx)x(f区间( a , b ) 中点值 mf ( m )的近似值精确度 |a-b|( 2 , 3 )2.5-0.0841( 2.5 , 3 )2.750.5120.5( 2.5 , 2.75 )2.6250.2150.25( 2.5 , 2.625 )2.562 50.0660.125( 2.5 , 2.562 5 )2.531 25-0.0090.0625( 2.531 25 , 2.562 5 )2.546 8750.0290.03125( 2.531 25 , 2.546 875 )2.539 062 50.010.015625( 2.531 25 , 2.539 062 5 )2.535 156 250.0010.007813 思考 4: 上述求函数零点近似值的方法叫做二分法,那么二分法的基本思想是什么? 对于在区间 [a , b] 上连续不断且 f(a)·f(b)<0 的函数 y=f(x) ,通过不断地把函数 f(x) 的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法 . 知识探究(二) :用二分法求函数零点近似值的步骤 2xy 3xy 思考 1: 求函数 f(x) 的零点近似值第一步应做什么? 思考 2: 为了缩小零点所在区间的范围,接下来应做什么? 确定区间 [a,b] ,使 f(a)f(b)<0 求区间的中点 c ,并计算 f(c) 的值 思考 3: 若 f(c)=0 说明什么? 若 f(a)·f(c)<0 或 f(c)·f(b)<0 ,则分别说明什么? 若 f(c)=0 ,则 c 就是函数的零点; 若 f(a)·f(c)<0 ,则零点 x0∈(a,c) ;若 f...