高中数学 立体几何中的向量方法一课件 新人教A版选修2 课件VIP免费

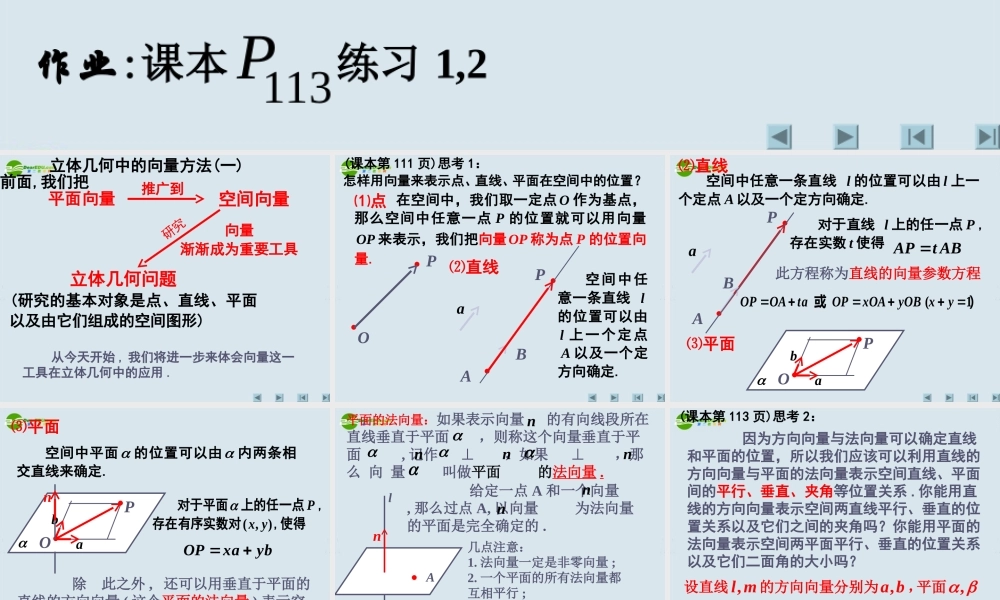
方向向量、法向量的运用思考练习引入知识要点本课小结作业:课本 113P练习 1,2 立体几何中的向量方法(一) 立体几何中的向量方法(一) 平面向量 空间向量 推广到 立体几何问题 (研究的基本对象是点、直线、平面以及由它们组成的空间图形) 向量 渐渐成为重要工具 研究 从今天开始 , 我们将进一步来体会向量这一工具在立体几何中的应用 .前面,我们把 在空间中，我们取一定点 O 作为基点，那么空间中任意一点 P 的位置就可以用向量OP�来表示，我们把向量OP�称为点 P 的位置向量. (课本第 111 页)思考 1： 怎样用向量来表示点、直线、平面在空间中的位置？ OP⑴点 ⑵直线 aABP空间中任意一条直线 l的位置可以由l 上一个定点A 以及一个定方向确定.  对于直线 l 上的任一点 P , 存在实数 t 使得 ⑵直线 aABP空间中任意一条直线 l 的位置可以由 l 上一个定点 A 以及一个定方向确定. APt AB�此方程称为直线的向量参数方程 (1OPOAtaOPxOAyOB xy�或）⑶平面 POba⑶平面 PObaOPxayb� 空间中平面 的位置可以由 内两条相交直线来确定. 对于平面 上的任一点 P , 存在有序实数对( , )x y ,使得 除 此之外 , 还可以用垂直于平面的直线的方向向量 ( 这个平面的法向量 ) 表示空间中平面的位置 .n 给定一点 A 和一个向量 , 那么过点 A, 以向量 为法向量的平面是完全确定的 .A平面的法向量：如果表示向量 的有向线段所在直线垂直于平面，则称这个向量垂直于平面 , 记作 ⊥ ，如果 ⊥ ，那 么 向 量 叫做平面 的法向量 .nnnnnnn几点注意：1. 法向量一定是非零向量 ;2. 一个平面的所有法向量都互相平行 ;3. 向量 是平面的法向量，向量 是与平面平行或在平面内，则有0n m��nm�l平行垂直(课本第 113 页)思考 2： 因为方向向量与法向量可以确定直线和平面的位置，所以我们应该可以利用直线的方向向量与平面的法向量表示空间直线、平面间的平行、垂直、夹角等位置关系 . 你能用直线的方向向量表示空间两直线平行、垂直的位置关系以及它们之间的夹角吗？你能用平面的法向量表示空间两平面平行、垂直的位置关系以及它们二面角的大小吗？设直线 ,l m 的方向向量分别为 ,a b，平面, 的法向量分别为 ,u v，则 夹角设直线 ,l m 的方向向量分...