高中数学 11正弦定理课件 苏教版必修5 课件VIP免费

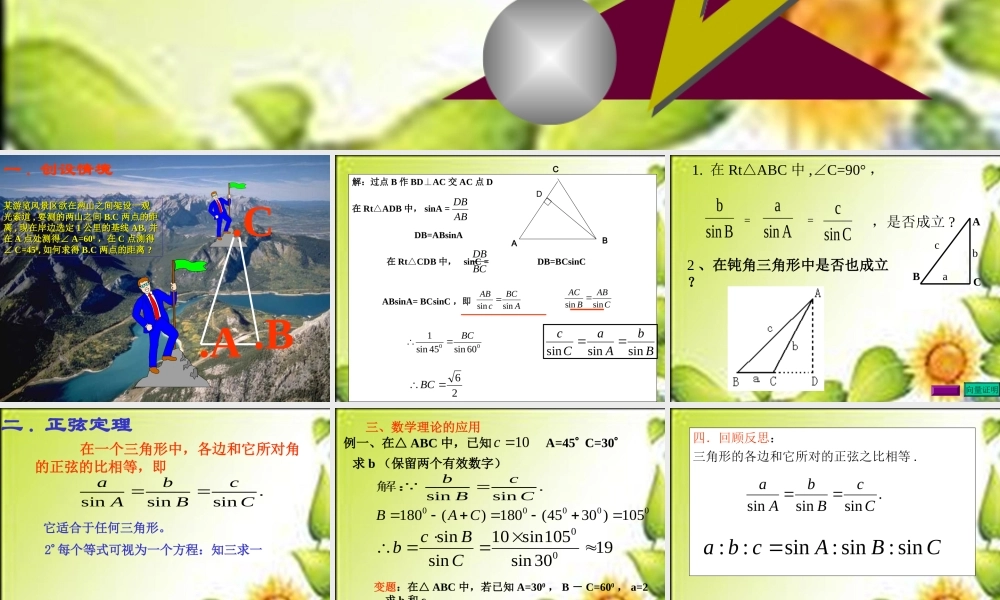
一 . 创设情境.B.A某游览风景区欲在两山之间架设一观某游览风景区欲在两山之间架设一观光索道光索道 ,, 要测的两山之间要测的两山之间 B.CB.C 两点的距两点的距离离 ,, 现在岸边选定现在岸边选定 11 公里的基线公里的基线 AB,AB, 并并在在 AA 点处测得∠点处测得∠ A=60A=6000 ，在，在 CC 点测得点测得∠∠ C=45C=4500,, 如何求得如何求得 B.CB.C 两点的距离两点的距离 ??.C解：过点 B 作 BDAC⊥交 AC 点 D在 RtADB△中， sinA = DB=ABsinA 在 RtCDB△中， sinC = DB=BCsinC ABsinA= BCsinC ，即ABDBBCDBABCcABsinsin0060sin45sin1BC26BCCABDCABBACsinsinBbAaCcsinsinsinAsinaBsinbCsinc1. 在 RtABC△中 ,C=90°∠，==，是否成立 ?BCAcba 2 、在钝角三角形中是否也成立？向量证明二 . 正弦定理 在一个三角形中，各边和它所对角的正弦的比相等，即.sinsinsinCcBbAa它适合于任何三角形。 2 每个等式可视为一个方程：知三求一 三、数学理论的应用 例一、在△ ABC 中，已知10cA=45 C=30 求 b （保留两个有效数字） 00000105)3045(180)(180CAB.sinsinCcBb解：1930sin105sin10sinsin00CBcb变题：在△ ABC 中，若已知 A=300 ， B － C=600 ， a=2，求 b 和 c四．回顾反思：三角形的各边和它所对的正弦之比相等 . CBAcbasin:sin:sin::.sinsinsinCcBbAa1 、一个三角形的两个内角分别为 300 和 450 ，如果 450 角所对的边长为 8 ，那么 300 角所对边的长为（ ）A 4 B C D 2 、在△ ABC 中（ 1 ）已知 A=750 ， B=450 ， c= 求 a ， b（ 2 ）已知 A=300 ， B=1200 ， b=12 ，求 a ， c4 24 34 63 2思考题1 ：在△ ABC 中， A=300 ， B=600 ， 则.____________::cba2 ．在半径为 2R 的圆内接△ ABC 中， 是否为定值 .sinsinsinabcABC课堂练习：五、作业 P11 页 1 、 2 、 3 、 4 题 .2006.4