2.3.1直线与平面垂直的判定VIP免费

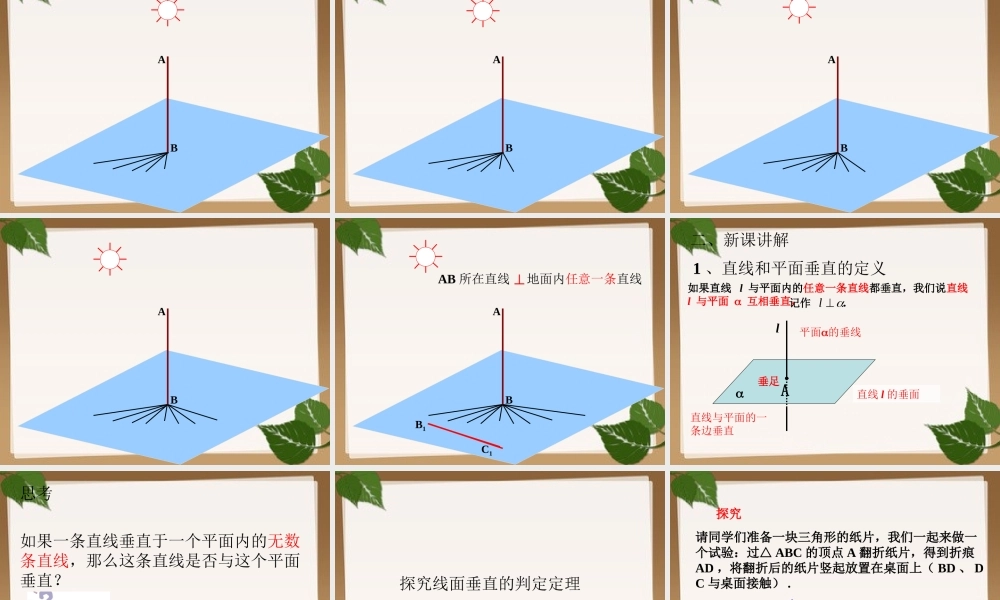
2.3.1 直线与平面垂直的判定 大城县第一中学 田蕊佳人民教育出版社 A 版 必修2教学目标： 1. 理解直线与平面的概念并通过实例 对线面垂直有初步的认识； 2. 掌握线面垂直的判定定理，并能够熟练运用； 3. 举一反三，培养学生的发散思维。一、复习回顾直线与平面的位置关系直线在平面内α aa直线与平面相交αAaAa直线与平面平行aα//a在直线和平面相交的位置关系中 , 有一种相交是很特殊的 , 我们把它叫做垂直相交 , 这节课我们重点来探究这种形式的相交 日常生活中，我们对直线和平面垂直有很多感性认识，比如天安门广场上矗立的旗杆与地面的位置关系，大桥的桥柱与水面的位置关系，都给我们以直线和平面垂直的形象。探究一下线面垂直的定义ABABABABABABABABC1B1AB地面内任意一条直线AB 所在直线⊥二、新课讲解1 、直线和平面垂直的定义l直线 l 的垂面A垂足如果直线 l 与平面内的任意一条直线都垂直，我们说直线 l 与平面  互相垂直，记作 ．l直线与平面的一条边垂直平面的垂线思考如果一条直线垂直于一个平面内的无数条直线，那么这条直线是否与这个平面垂直？BC不一定探究线面垂直的判定定理请同学们准备一块三角形的纸片，我们一起来做一个试验：过△ ABC 的顶点 A 翻折纸片，得到折痕AD ，将翻折后的纸片竖起放置在桌面上（ BD 、 DC 与桌面接触） .ABCD探究(1) 折痕 AD 与桌面垂直吗？ABDC(2) 如何翻折才能保证折痕 AD 与桌面所在平面α 垂直？ABDCABDCABDCABDCABDCABDCABDCABDCABDCABDC当折痕 ADBC⊥且翻折后 BD 与 DC 不在一条直线上时 , 折痕 AD 与桌面所在平面垂直 .ABDC 一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直．2、直线和平面垂直的判定定理符号表示：,,mnmnPllm ln线线垂直 线面垂直lmnP3 、线面垂直的判定定理的应用例 1 ：如图，在四棱锥 P-ABCD 中，底面 ABCD 为菱形，PA=PC,PB=PD,AC 交 BD 于点 O ，（ 1 ）求证： PO ⊥ 平面 ABCD（ 2 ）求证： AC ⊥ 平面 PBDABCDPO证明（ 1 ） PA=PC ， O 为 AC中点 ∴POAC. ⊥ PB=PD ， O 为 BD 中点 ∴POBD⊥ 又 AC∩BD=O ∴PO ⊥ 平面 ABCD例 1 ：如图，在四棱锥 P-ABCD 中，底面 ABCD 为菱形，PA=PC,PB=PD,AC 交 BD 于点 O ，（ 1 ）求证： PO ⊥ 平面 ABCD（...