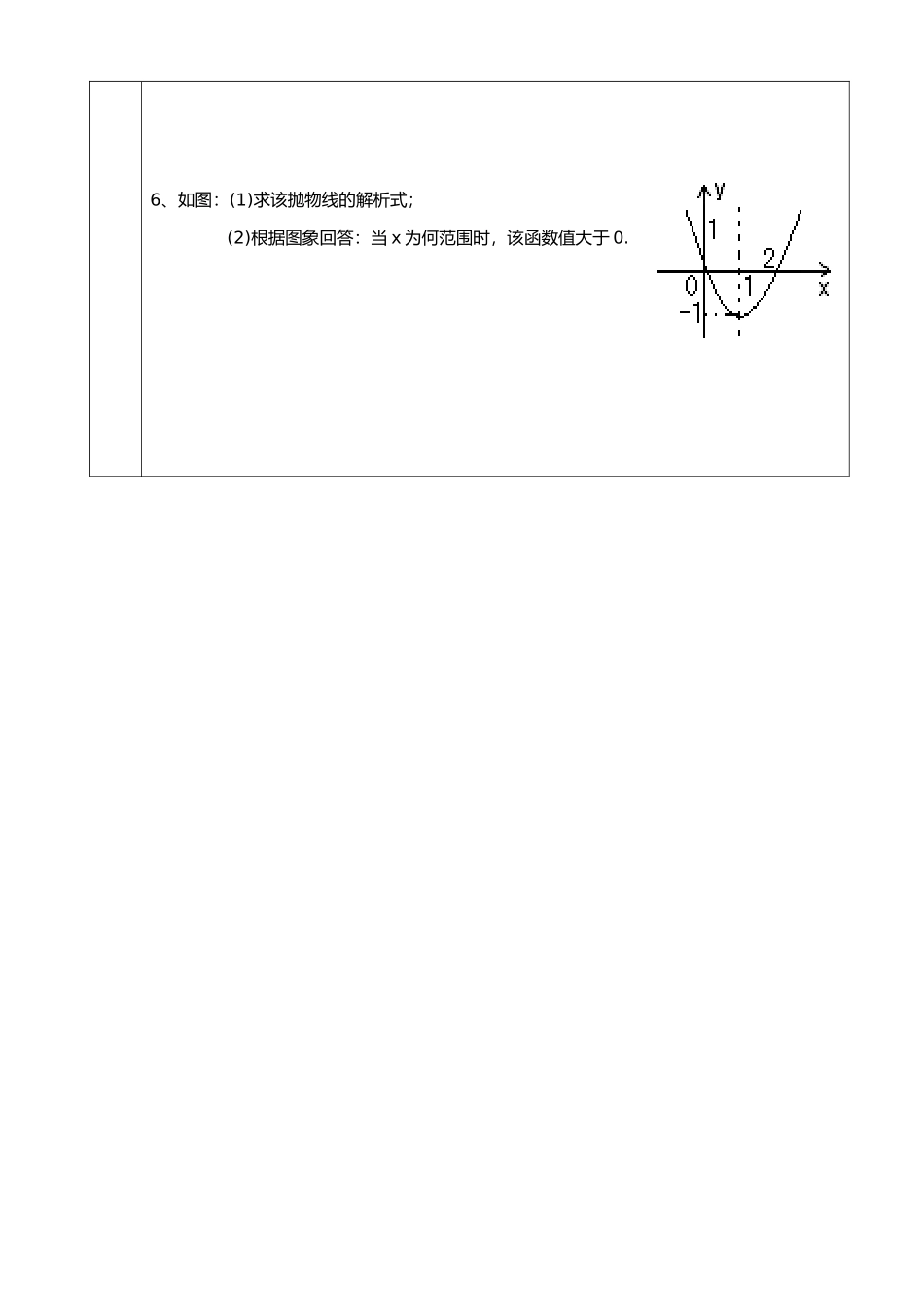
九年级数学课堂练习及检测表 课题:二次函数(四) 第 1 课时(总第 43 课时) 姓名: 上课日期:2014.10.27重点二次函数解析式;二次函数与方程和不等式关系。难点二次函数与方程和不等式关系。基础知识1.抛物线解析式三种表达方式:一般式y=ax2+bx+c; 顶点式y=a (x−h)2+k;交点式;2.二次函数与其所对应的一元二次方程之间关系:课前练习1、抛物线 y=ax2+bx+c 经过 A(-1,0), B(3,0), C(0,1)三点,则 a= , b= , c= 2、把抛物线 y=x2+2x-3 向左平移 3 个单位,然后向下平移 2 个单位,则所得的抛物线的解析式为 .3、已知二次函数y=kx2−7 x−7 与 x 轴有交点,则 k 的取值范围是 .课堂1、二次函数有最小值为,当时,,它的图象的对称轴为,则函数的关系式为 2、关于 x 的一元二次方程x2−x−n=0没有实数根,则抛物线y=x2−x−n 的顶点在第_____象限;3、y=x2+kx+1与y=x2−x−k 的图象相交,若有一个交点在 x 轴上,则 k 为( )练习A、0 B、-1 C、2 D、144、已知抛物线. (1)求证此抛物线与轴有两个不同的交点; (2)若是整数,抛物线与轴交于整数点,求的值;巩固练习1、已知二次函数的图象经过、两点,且与轴仅有一个交点,求二次函数的解析式2、抛物线y=−x2+2kx+2与x 轴交点的个数为( )A、0 B、1 C、2 D、以上都不对3、二次函数y=ax2+bx+c 对于 x 的任何值都恒为负值的条件是( )A、a>0, Δ>0 B、a>0, Δ<0 C、a<0, Δ>0 D、a<0, Δ<04、若方程ax 2+bx+c=0的两个根是-3 和 1,那么二次函数y=ax2+bx+c 的图象的对称轴是直线( )A、x =-3 B、x =-2 C、x =-1 D、x =15、已知二次函数的图象与轴只有一个公共点,坐标为,求的值6、如图:(1)求该抛物线的解析式;(2)根据图象回答:当 x 为何范围时,该函数值大于 0.