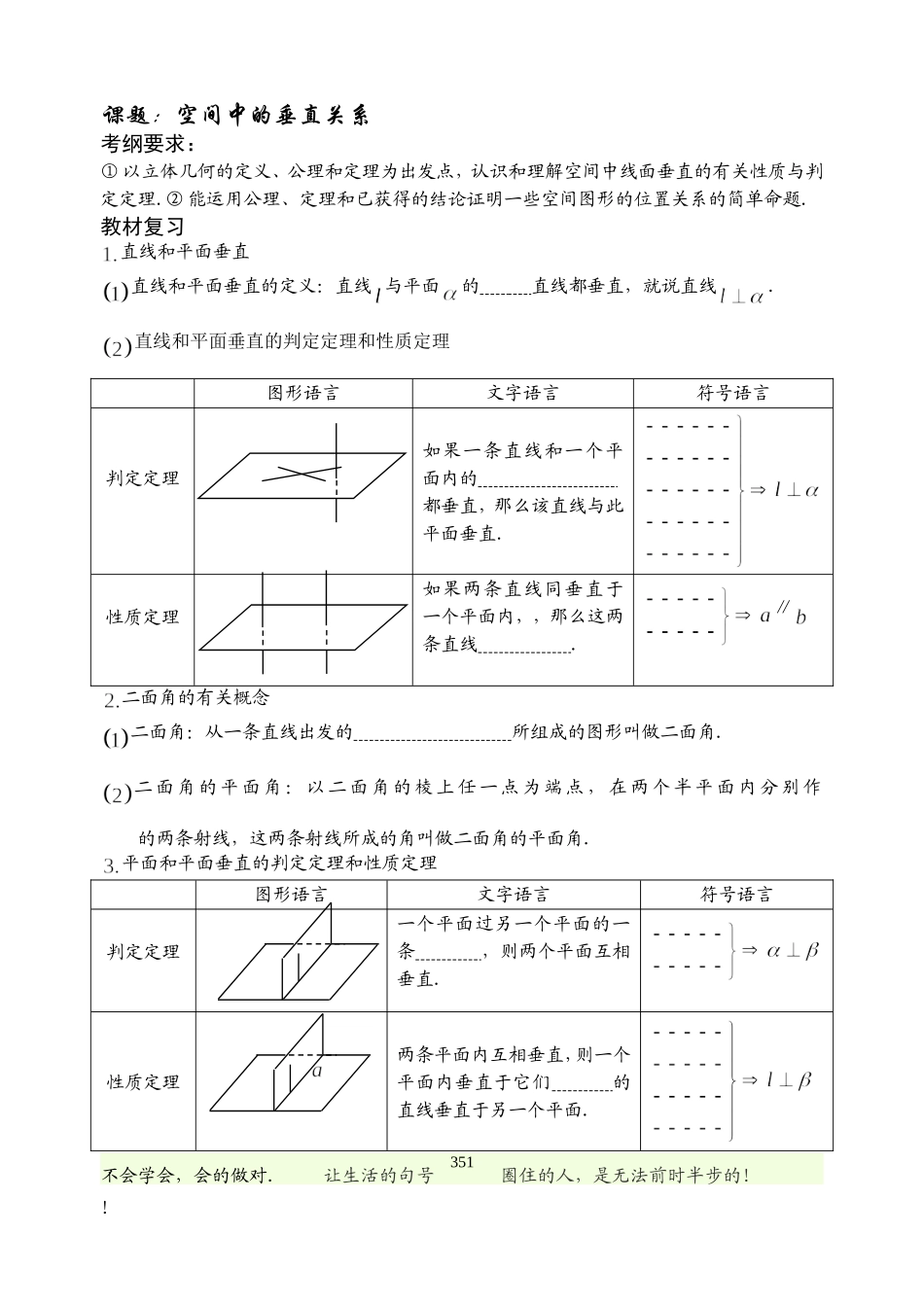
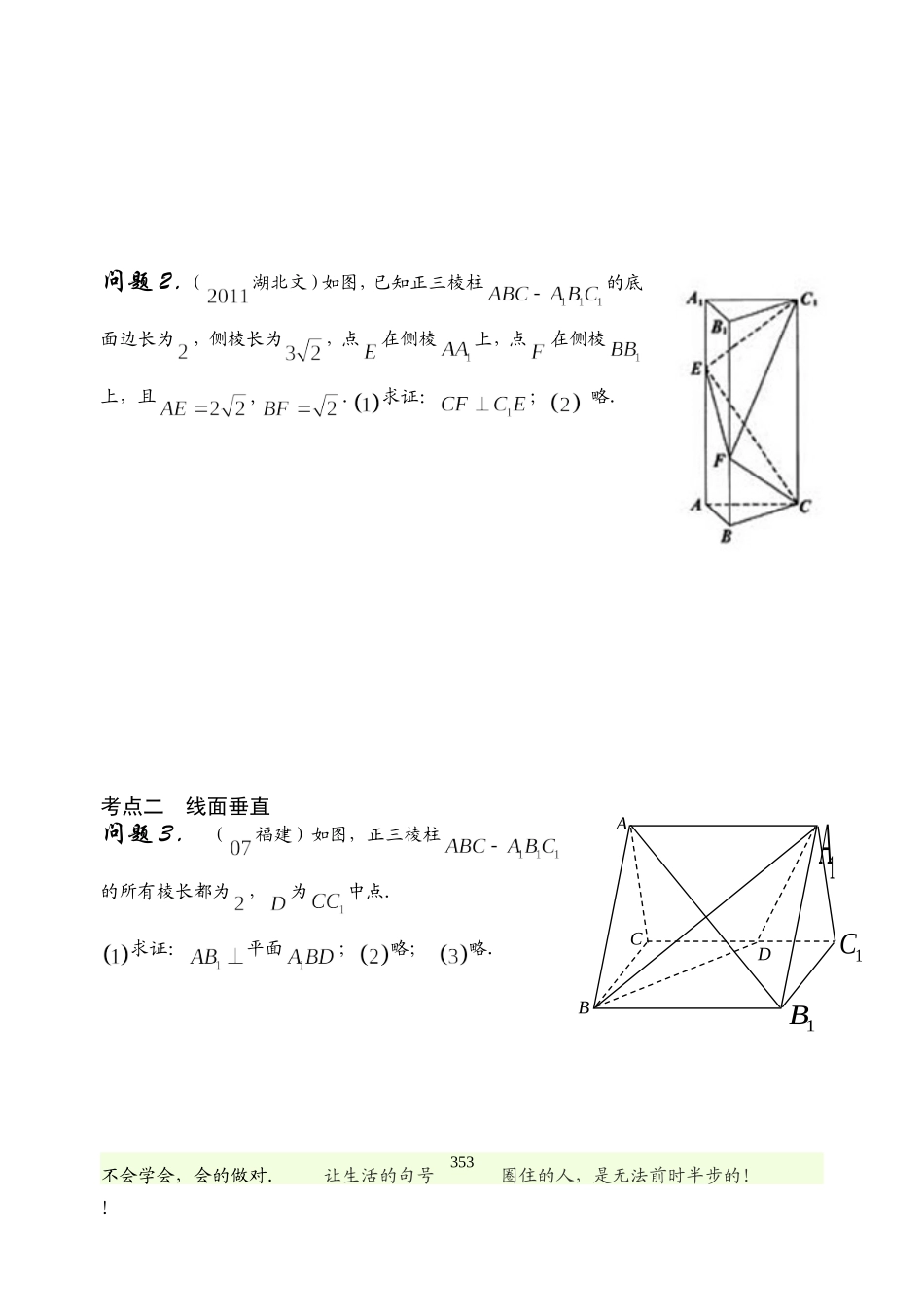
课题:空间中的垂直关系考纲要求:① 以立体几何的定义、公理和定理为出发点,认识和理解空间中线面垂直的有关性质与判定定理.② 能运用公理、定理和已获得的结论证明一些空间图形的位置关系的简单命题.教材复习直线和平面垂直直线和平面垂直的定义:直线 与平面的 直线都垂直,就说直线.直线和平面垂直的判定定理和性质定理图形语言文字语言符号语言判定定理如果一条直线和一个平面内的 都垂直,那么该直线与此平面垂直.性质定理如果两条直线同垂直于一个平面内,,那么这两条直线 .∥二面角的有关概念二面角:从一条直线出发的 所组成的图形叫做二面角.二 面 角 的 平 面 角 : 以 二 面 角 的 棱 上 任 一 点 为 端 点 , 在 两 个 半 平 面 内 分 别 作 的两条射线,这两条射线所成的角叫做二面角的平面角.平面和平面垂直的判定定理和性质定理图形语言文字语言符号语言判定定理一个平面过另一个平面的一条 ,则两个平面互相垂直.性质定理两条平面内互相垂直,则一个平面内垂直于它们 的直线垂直于另一个平面.不会学会,会的做对. 让生活的句号 圈住的人,是无法前时半步的!! 351基本知识方法 证明线面垂直的方法(1)线面垂直的定义:a 与 α 内任何直线都垂直;(2)判定定理 :;(3)判定定理:a∥b, ;(4)面面平行的性质:∥,⇒;(5)面面垂直的性质:,,, 证明直线与平面的法向量平行.证明线线垂直的方法(1)定义:两条直线所成的角为;(2)平面几何中证明线线垂直的方法;(3)线面垂直的性质:,;(4)线面垂直的性质:,∥. 证明两直线的方向向量互相垂直.证明面面垂直的方法(1)利用定义:两个平面相交,所成的二面角是直二面角;(2)判定定理:, ⇒.证明两平面的法向量垂直.转化思想:垂直关系的转化(右图).在证明两平面垂直时一般先从现有的直线中寻找平面的垂线,若这样的直线图中不存在,则可通过作辅助线来解决.典例分析:考点一 线线垂直问题 1. (天津)如图, 四棱柱中, 侧棱底面, ∥,, , , 为棱的中点. (Ⅰ)求证:; (Ⅱ)略. (Ⅲ)略. 不会学会,会的做对. 让生活的句号 圈住的人,是无法前时半步的!! 352问题 2.(湖北文)如图,已知正三棱柱的底面边长为,侧棱长为,点在侧棱上,点在侧棱上,且,.求证:; 略. 考点二 线面垂直问题 3. (福建)如图,正三棱柱的所有棱长都为,为中点.求证:平面;略; 略.不会学会,会的做对. 让生活的句号 ...