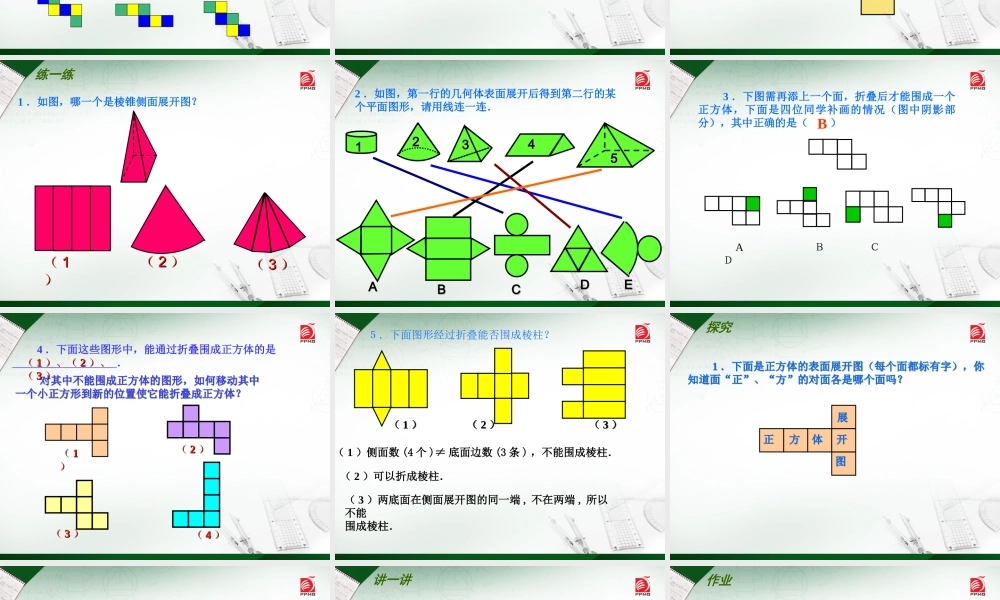
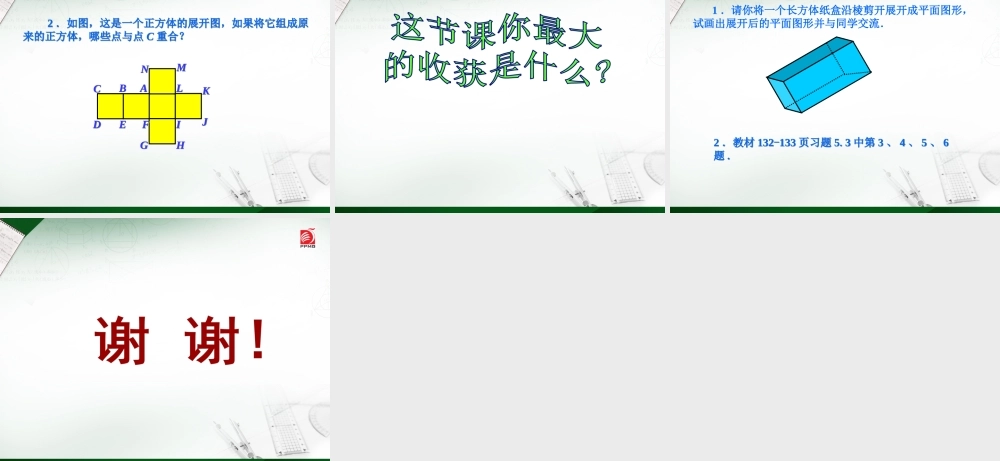
5.3 展开与折叠七年级 ( 上册 ) 初中数学 你会将下列几何体展开成平面图形吗?画出示意图.想一想 想一想 圆柱的表面展开图是:两个圆 ( 作底面 ) 和一个长方形 ( 作侧面 ) . 圆锥的表面展开图是:一个圆 ( 作底面 ) 和一个扇形( 作侧面 ) . 如何把一个正方体的表面沿棱剪开,展开成一个平面图形?分组讨论并尝试剪一剪. 如何把一个正方体的表面沿棱剪开,展开成一个平面图形?分组讨论并尝试剪一剪. 做一做 做一做 注意:剪开正方体棱的过程中,正方体的 6 个面中每个面至少有一条棱与其他面相连 . 注意:剪开正方体棱的过程中,正方体的 6 个面中每个面至少有一条棱与其他面相连 . 将一个正方体沿棱剪开 , 并展开成一个平面图形,你能得到哪些图形?秀一秀 秀一秀 你能展开成下面的图形吗?试试看. 你能展开成下面的图形吗?试试看. ①②③④⑤ 2 .要将一个正方体纸盒的表面展开成一个平面图形,要剪开多少条棱?思考: 思考: 1 .同一种正方体纸盒沿不同顺序先后剪开棱展开的平面图形是否相同? 1 .同一种正方体纸盒沿不同顺序先后剪开棱展开的平面图形是否相同? 1 .如图,哪一个是棱锥侧面展开图?(( 11))(( 22 ))(( 33 ))练一练 练一练 2 .如图,第一行的几何体表面展开后得到第二行的某个平面图形,请用线连一连.22334455AABBCCDDEE11 3 .下图需再添上一个面,折叠后才能围成一个正方体,下面是四位同学补画的情况(图中阴影部分),其中正确的是( ) A B C DB 4 .下面这些图形中,能通过折叠围成正方体的是 .(( 11))(( 44 ))(( 33 ))(( 22 )) 对其中不能围成正方体的图形,如何移动其中一个小正方形到新的位置使它能折叠成正方体? 对其中不能围成正方体的图形,如何移动其中一个小正方形到新的位置使它能折叠成正方体? (( 11 )、()、( 22 )、)、(( 33 ))5.下面图形经过折叠能否围成棱柱?( 2 )可以折成棱柱. ( 1 )侧面数 (4 个 )≠ 底面边数 (3 条 ) ,不能围成棱柱. ( 3 )两底面在侧面展开图的同一端 , 不在两端 , 所以不能围成棱柱.( 1 )( 1 )( 2 )( 2 )( 3 )( 3 ) 1 .下面是正方体的表面展开图(每个面都标有字),你知道面“正”、“方”的对面各是哪个面吗? 1 .下面是正方体的表面展开图(每个面都标有字)...