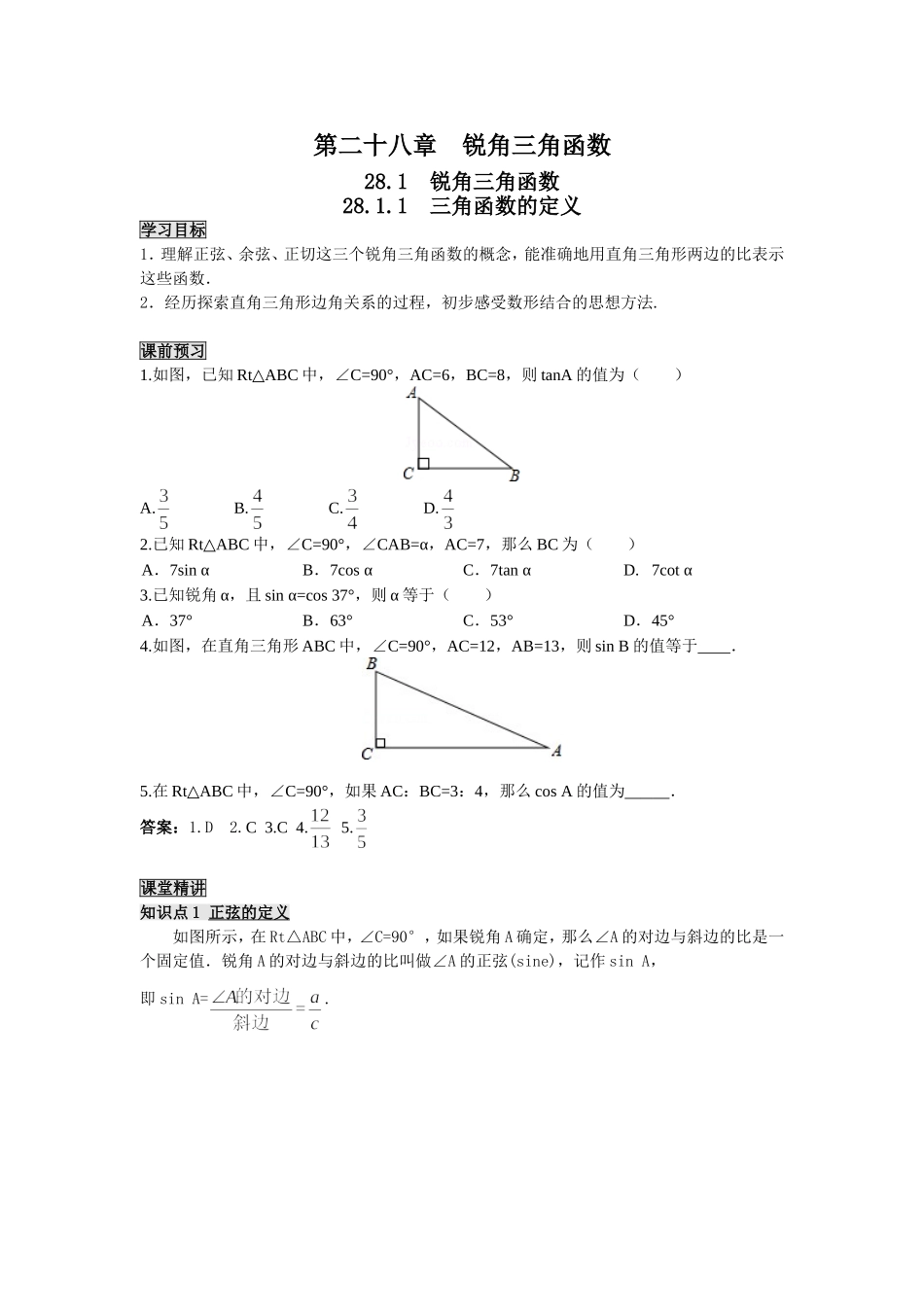
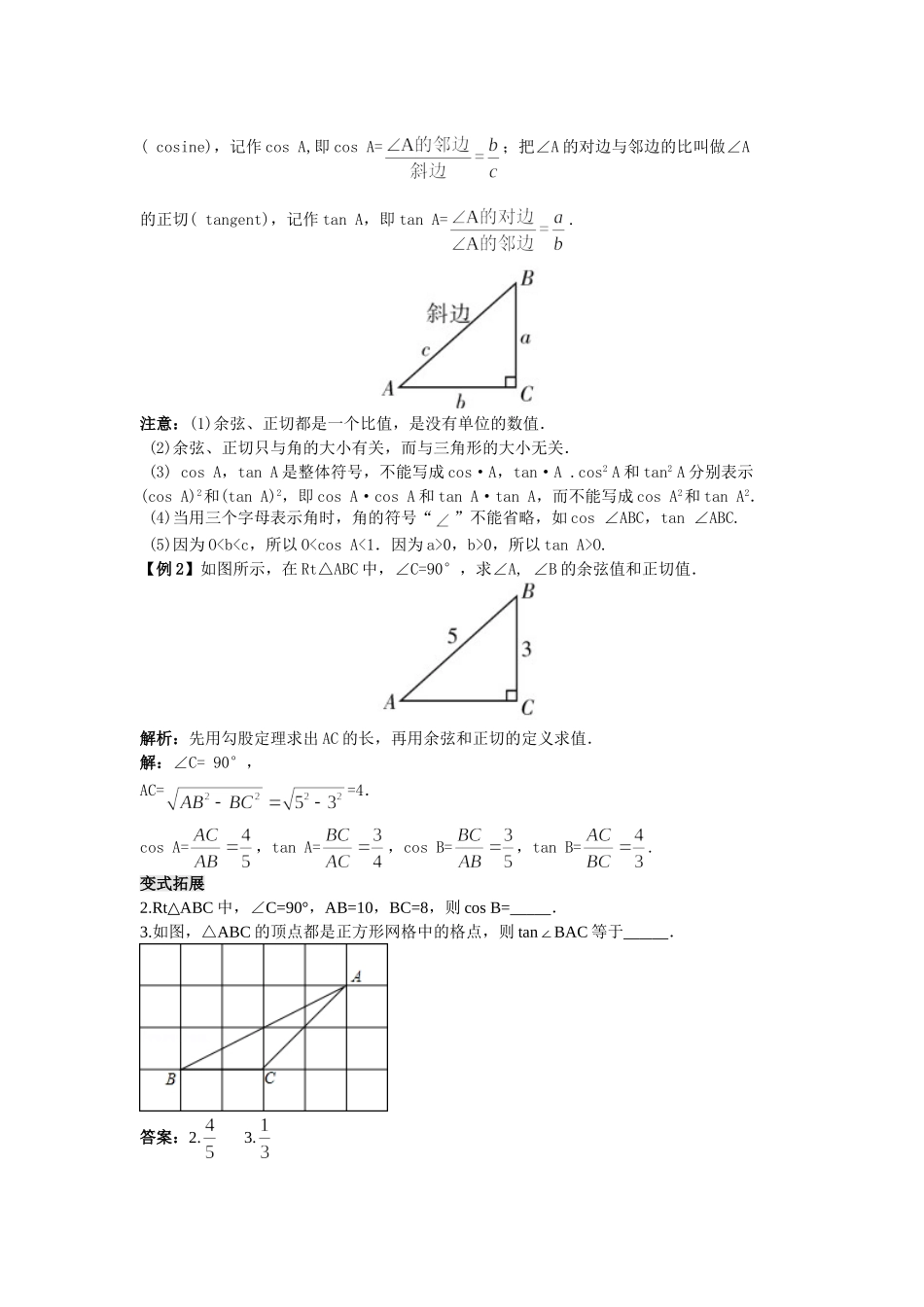
第二十八章 锐角三角函数28.1 锐角三角函数28.1.1 三角函数的定义学习目标1.理解正弦、余弦、正切这三个锐角三角函数的概念,能准确地用直角三角形两边的比表示这些函数.2.经历探索直角三角形边角关系的过程,初步感受数形结合的思想方法.课前预习1.如图,已知 Rt ABC△中,∠C=90°,AC=6,BC=8,则 tanA 的值为( )A. B. C. D.2.已知 Rt ABC△中,∠C=90°,∠CAB=α,AC=7,那么 BC 为( ) A.7sin αB.7cos αC.7tan αD. 7cot α3.已知锐角 α,且 sin α=cos 37°,则 α 等于( ) A.37°B.63°C.53°D.45°4.如图,在直角三角形 ABC 中,∠C=90°,AC=12,AB=13,则 sin B 的值等于 .5.在 Rt ABC△中,∠C=90°,如果 AC:BC=3:4,那么 cos A 的值为 .答案:1.D 2.C 3.C 4. 5.课堂精讲知识点 1 正弦的定义如图所示,在 Rt△ABC 中,∠C=90°,如果锐角 A 确定,那么∠A 的对边与斜边的比是一个固定值.锐角 A 的对边与斜边的比叫做∠A 的正弦(sine),记作 sin A,即 sin A=. 注意:(1)正弦是在直角三角形中定义的,反映了直角三角形边与角的关系,是两条线段的比值,它没有单位,当角的度数确定时,其比值随之确定,与三角形的边的长短无关,即与三角形的大小无关. (2) sin A 是一个完整的符号,不能写成“sin·A”,书写时习惯省略∠A 的角的符号“∠”,但当用三个大写字母表示角时(如∠ABC),其正弦应写成 sin ∠ABC,不能写成 sin ABC. sin2 A 表示(sin A)2,即 sin A·sin A,而不能写成 sin A2. (3)在直角三角形中,因为 O