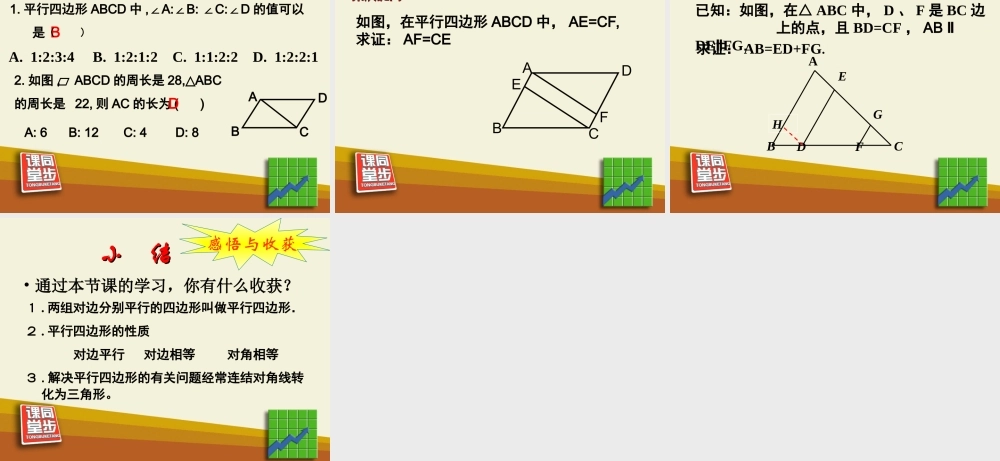
平行四边形的性质下面的图片中,有你熟悉的图形吗?什么样的四边形是平行四边形 ?两组对边分别平行的四边形叫做平行四边形两组对边分别平行的四边形叫做平行四边形 ..读作:平行四边形读作:平行四边形 ABCDABCDAADDBBCC记作: 记作: ABCDABCDAB∥CDAB∥CDAD∥BCAD∥BC∵∴∴ 四边形四边形 ABCDABCD 是平行四边是平行四边形形∵∵ 四边形四边形 ABCDABCD 是是平行四边形平行四边形AB∥CDAB∥CDAD∥BCAD∥BC∴ 理解定义平行四边形的对边相等.平行四边形的对角相等.(1) 平行四边形的对边有什么数量关系 ?(2) 平行四边形的对角有什么数量关系?利用准备好的平行四边形纸片验证你的猜想 方法一: 用直尺 , 量角器 方法二: 剪AC=CA ∴ AB=CD 、BC=AD证明:连接AC∵ 四边形 ABCD 是平行四边形 ∴ AD ∥∥BC AB ∥∥CD ∴ ∠2=3 4=1∠∠∠在 ABC 和 CDA 中∠4=1∠∠2=3∠ ABC≌ CDA ( ASA ) : AD=BC AB=CD: ABCDADCB4231小结:作对角线是解决四边形问题常用的小结:作对角线是解决四边形问题常用的 辅助线,通过作对角线把未知的辅助线,通过作对角线把未知的四四 边形问题转化为熟知三角形问边形问题转化为熟知三角形问题题 ..已知求证2. 平行四边形的对角相等 .∵ ABCD1. 平行四边形的对边相等;∵ ABCD∴AB=CD , AD=BC∴∠A =∠ C,∠B =∠ D平行四边形的性质小结:平行四边形的性质是证明线段相等和角相等的重要依据和方法。 如图 : 在 ABCD 中 , 根据已知你能得到哪 些结论?为什么 ?4cm5cm4cmABCD50°50°130°130°5cm例 1 如图,小明用一根 36m 长的绳子围成了一个平行四边形的场地,其中一条边 AB 长为 8m. 解 : ABCD∵ 求其他三条边各长多少?8m∴AB=CD,AD=BC.∴AB=CD=8m∴AD=BC=10(m).又∵ AB+BC+CD+AD=36, A. 1:2:3:4 B. 1:2:1:2 C. 1:1:2:2 D. 1:2:2:1BABDC2. 如图 , ABCD 的周长是 28, ABC△的周长是 22, 则 AC 的长为 ( )A: 6 B: 12 C: 4 D: 8D1. 平行四边形 ABCD 中 ,A:B: C:D∠∠∠∠的值可以 是﹙ ﹚如图,在平行四边形 ABCD 中, AE=CF,求证: AF=CEAFEDCB已知:如图,在△ ABC 中, D 、 F 是 BC 边 上的点,且 BD=CF , AB ‖DE‖FG.ABCEDGFH求证: AB=ED+FG.• 通过本节课的学习,你有什么收获?1 . 两组对边分别平行的四边形叫做平行四边形.2 . 平行四边形的性质 对边平行 对边相等 对角相等3 . 解决平行四边形的有关问题经常连结对角线转感悟与收获小 结小 结化为三角形。