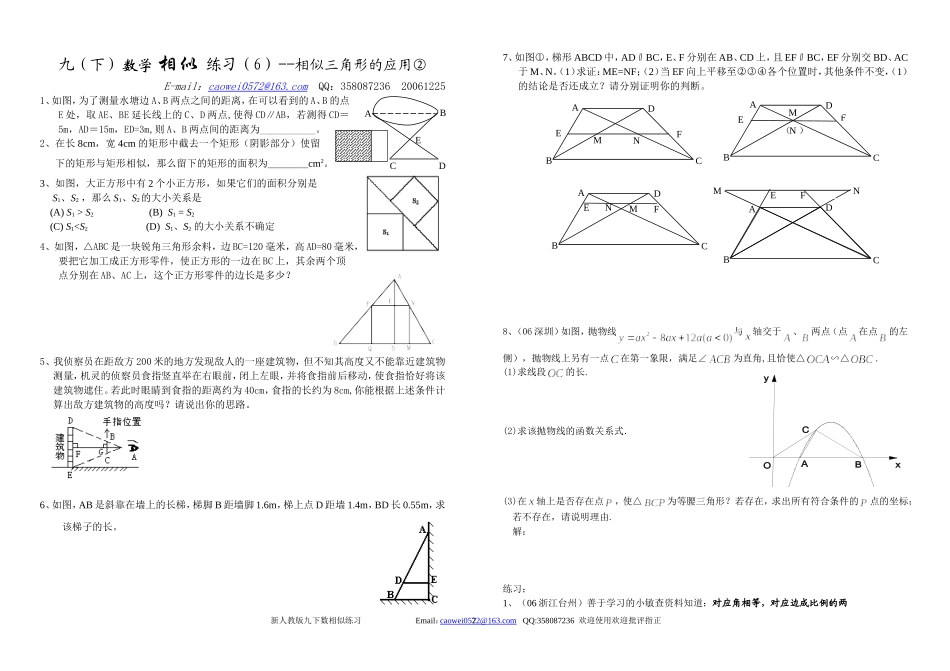
九(下)数学 相似 练习(5)--相似三角形的应用①E-mail:caowei0572@163.com QQ:358087236 20061223 1、在阳光下,身高 1.68m 的小强在地面上的影长为 2m,在同一时刻,测得学校的旗杆在地面上的影长为 18m.则旗杆的高度为 (精确到 0.1m).2、如图,在河两岸分别有 A、B 两村,现测得 A、B、D 在一条直线上,A、C、E在一条直线上,BC//DE,DE=90 米,BC=70 米,BD=20 米。则 A、B 两村间的距离为 。3、(06 湖州)为了测量校园水平地面上一棵不可攀的树的高度,学校数学兴趣小组做了如下的探索:根据《科学》中光的反射定律,利用一面镜子和一根皮尺,设计如下图所示的测量方案:把一面很小的镜子放在离树底(B)8.4 米的点 E 处,然后沿着直线 BE 后退到点 D,这时恰好在镜子里看到树梢顶点 A,再用皮尺量得DE=2.4 米,观察者目高 CD=1.6 米,则树(AB)的高度约为________米(精确到 0.1 米)。4、如图,某测量工作人员与标杆顶端 F、电视塔顶端在同一直线上,已知此人眼睛距地面 1.6 米,标杆为 3.2 米,且 BC=1 米,CD=5米,求电视塔的高 ED。5、小强用这样的方法来测量学校教学楼的高度:如图,在地面上放一面镜子(镜子高度忽略不计),他刚好能从镜子中看到教学楼的顶端 B,他请同学协助量了镜子与教学楼的距离EA=21 米,以及他与镜子的距离 CE=2.5 米,已知他的眼睛距离地面的高度 DC=1.6 米,请你帮助小强计算出教学楼的高度。(根据光的反射定律:反射角等于入射角)6、某数学课外实习小组想利用树影测量树高,他们在同一时刻测得一身高为 1.5 米的同学的影子长为 1.35 米,因大树靠近一栋建筑物,大树的影子不全在地面上,他们测得地面部分的影子长BC=3.6 米,墙上影子高 CD=1.8 米,求树高 AB。7、如图,甲楼 AB 高 18 米,乙楼坐落在甲楼的正北面,已知当地冬至中午12 时,物高与影长的比是 1: ,已知两楼相距 20 米,那么甲楼的影子落在乙楼上有多高?8、为了测量路灯(OS)的高度,把一根长 1.5 米的竹竿(AB)竖直立在水平地面上,测得竹竿的影子(BC)长为 1 米,然后拿竹竿向远离路灯方向走了 4 米(BB‘),再把竹竿竖立在地面上, 测得竹竿的影长(B‘C‘)为 1.8 米,求路灯离地面的高度.9、如图,有一路灯杆 AB(底部 B 不能直接到达),在灯光下,小明在点 D 处测得自己的影长 DF=3m,沿 BD 方向到达点 F 处再测得自己得影长 FG=4m,如果小明...