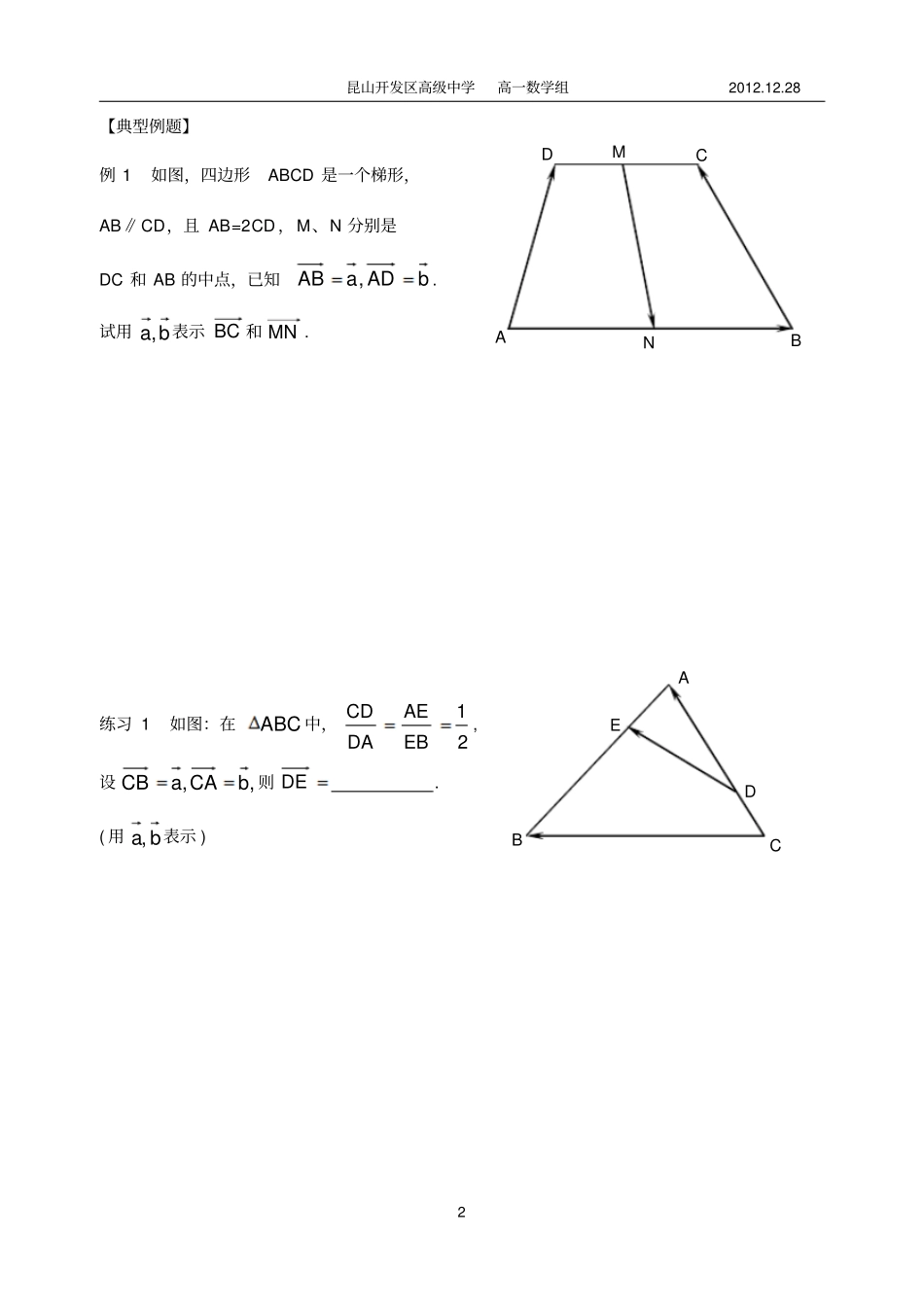
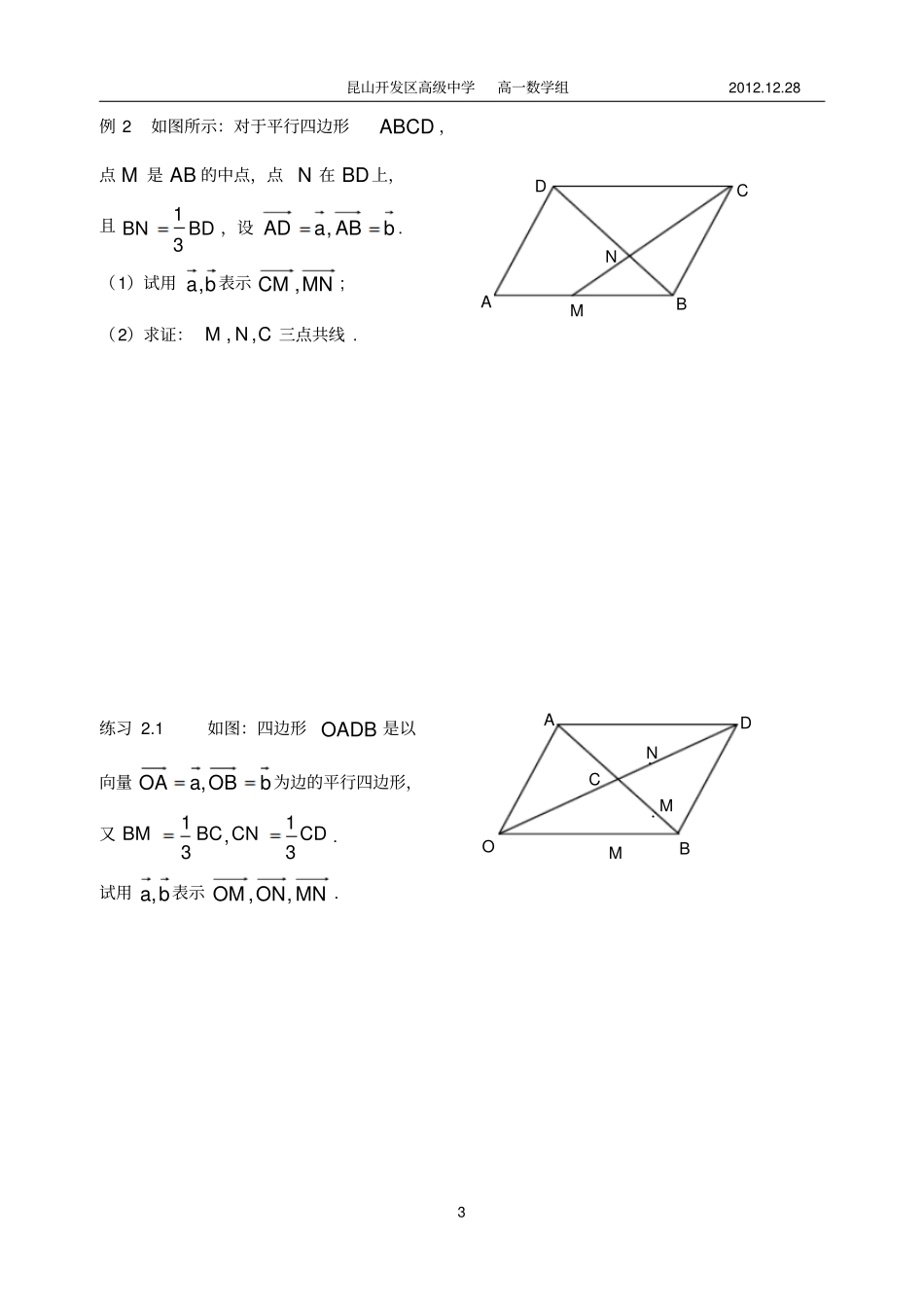
昆山开发区高级中学高一数学组2012.12.28 1 向量的线性运算习题课昆山开发区高级中学何静【学习目标】1. 掌握向量加法、减法的运算法则及运算律. 2. 掌握向量的数乘及运算律;理解并掌握向量的共线定理. 3.向量线性运算的综合应用. 【重点难点】向量线性运算的综合应用. 【课前小练】1. 已知正方形 ABCD 的边长为 a ,则ACBCAB; BCADAB2. 2. 已知平行四边形OACB 的两邻边,,bOBaOA其对角线的交点为D ,则 OD( 用ba,表示 ).3. 如图:已知 O 为正六边形 ABCDEF 的中心 , ,,OBbOFa则 EF. 4. 若,3,,2121PPPPbOPaOP则 OP ( 用ba,表示 ).5. 已知,2,2,2baba则ba. A F E C B D O 昆山开发区高级中学高一数学组2012.12.28 2 【典型例题】例 1 如图,四边形ABCD 是一个梯形,AB∥CD,且 AB=2CD ,M、N 分别是DC 和 AB 的中点,已知bADaAB,. 试用ba,表示 BC 和 MN . 练习 1 如图:在ABC 中,21EBAEDACD, 设,,bCAaCB则 DE. ( 用ba,表示 ) B C A D E D A M N B C 昆山开发区高级中学高一数学组2012.12.28 3 例 2 如图所示:对于平行四边形ABCD ,点 M 是 AB 的中点,点 N 在 BD上,且13BNBD ,设bABaAD,. (1)试用ba,表示MNCM ,; (2)求证:,,M N C 三点共线 . 练习 2.1 如图:四边形 OADB 是以向量bOBaOA,为边的平行四边形,又CDCNBCBM31,31. 试用ba,表示MNONOM,,.A B C D M N ··O B D A C M N M 昆山开发区高级中学高一数学组2012.12.28 4 练习 2.2 如图,在平行四边形ABCD 中,点 M在 AB 的延长线上,且12BMAB, 点 N 在 BC 上,且13BNBC ,设bADaAB,. 用向量法证明 : M 、 N 、 D 三点共线 . 【拓展提高】已知△ ABC 中, D 为 BC 中点, E、F 为AC、BA 的中点, AD、BE、CF、相交于 O 点,求证:(1))(21ACABAD;(2)0CFBEAD;(3)0OCOBOA. A B C D M N B D F C O E A