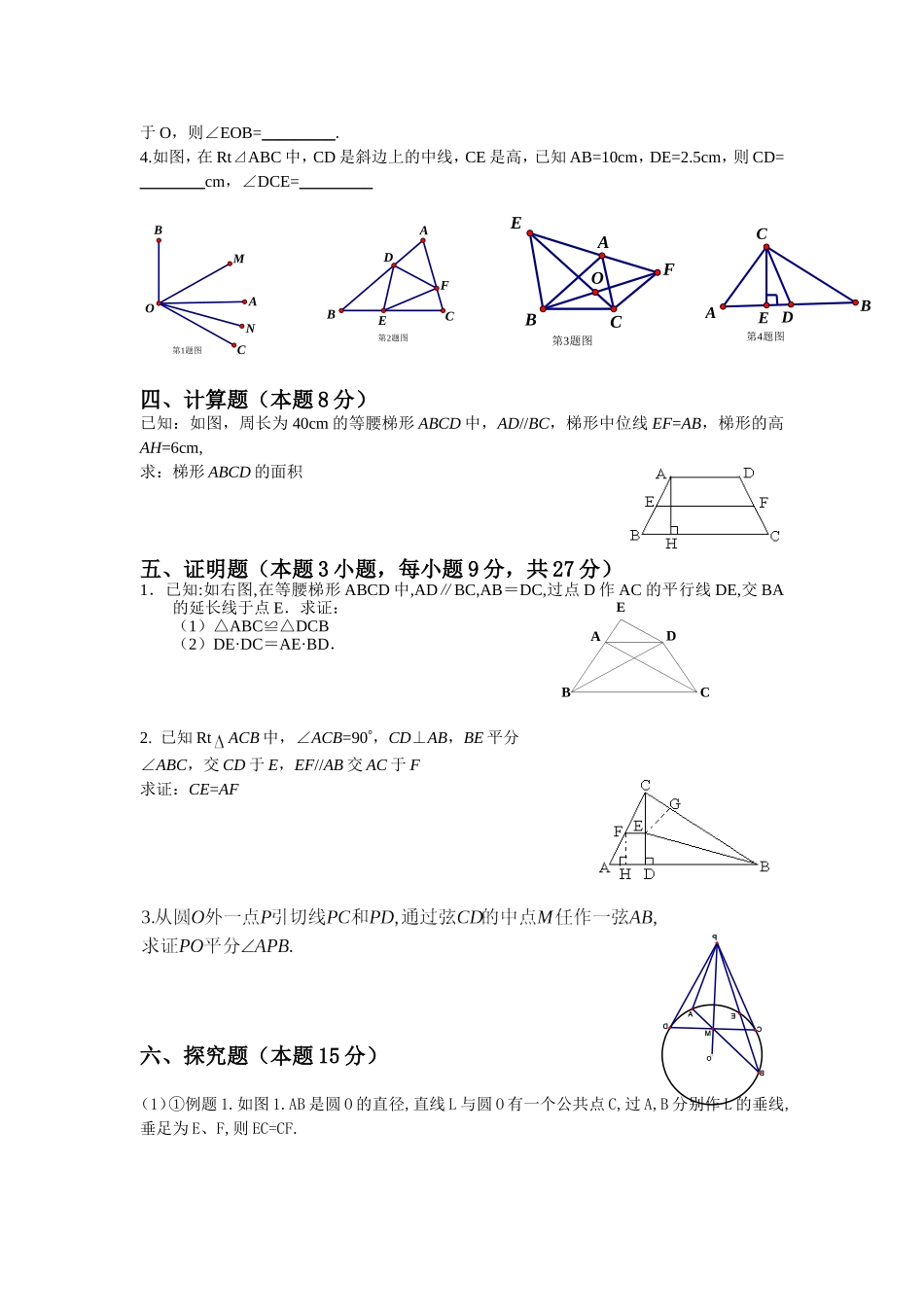
《初等几何研究》综合测试题(四)适用专业:数学教育专业考试时间:120分钟一、选择题(本题共8小题,每小题3分,共24分)1.如果三角形的一个角等于其他两个角的差,则这个三角形一定是________。A.等腰三角形;B.锐角三角形;C.直角三角形;D.钝角三角形。2.在棱形、矩形、等腰梯形和直角梯形中,对角线相等的四边形有_________A.1个;B.2个;C.3个;D.4个。3.等腰梯形的一角为45°,高为2m,中位线为6m,则上底长为_______.A.8m;B.4m;C.2m;D.1m。4.如图,如果梯形的两条对角线分中位线为3等分,那么梯形上、下底之比为________。A.1:2;B.1:3;C.2:3;D.3:5。5.如果ad=bc(abcd≠0),那么下列比例中错误的是_______.A.;B.;C.;D.。6.下列不正确的命题是_________。A.弦切角所夹的为等弧,则弦切角相等。B.弦切角的度数等于它所夹弧度数一半。C.弦切角等于它夹弧所对圆心角的一半。D.弦切角相等,则它们所夹的弧也相等。7.在平移过程中,对应线段A.互相平行且相等;B.互相垂直且相等;C.互相平行(或在同一条直线上)且相等;D.以上都不对。8.下列关于平移的说法中正确的是___________。A.原图形中两个顶点连成的线段长是平移的距离;B.平移后的两个图形中两个顶点连成的线段长是平移的距离;C.以对应点中的一点为端点的射线是平移的方向。D.以原图形中的一点为端点,且经过它的对应点的射线的方向是平移的方向;二、判断题(本题共5小题,每小题2分,共10分)1.若两条直线同垂直于第三条直线,则这两条直线平行。()2.有两边和一角对应相等的两个三角形全等。()3.两条对角线分别平分两组对角的四边形是棱形。()4.两条对角线互相垂直且有一条对角线平分一组对角的四边形是棱形。()5.由三条线段首尾连接围成的封闭图形叫做三角形。()三、填空题(本题共4小题,每小题4分,共16分)1.如图,∠AOB=90°,∠AOC为锐角,ON平分∠AOC,OM平分∠BOC,则∠MON的度数是__________.2.在⊿ABC的各边AB、BC、CA上取AD、BE、CF各等于边的,则的值等于_________。3.如图,⊿ABE和⊿ACF分别是以⊿ABC德AB,AC为边在形外的正三角形,CE、BF相交第4题图NMFEADBCABCED于O,则∠EOB=_________.4.如图,在Rt⊿ABC中,CD是斜边上的中线,CE是高,已知AB=10cm,DE=2.5cm,则CD=________cm,∠DCE=_________四、计算题(本题8分)已知:如图,周长为40cm的等腰梯形ABCD中,AD//BC,梯形中位线EF=AB,梯形的高AH=6cm,求:梯形ABCD的面积五、证明题(本题3小题,每小题9分,共27分)1.已知:如右图,在等腰梯形ABCD中,AD∥BC,AB=DC,过点D作AC的平行线DE,交BA的延长线于点E.求证:(1)△ABC≌△DCB(2)DE·DC=AE·BD.2.已知RtACB中,∠ACB=90,CD⊥AB,BE平分∠ABC,交CD于E,EF//AB交AC于F求证:CE=AF六、探究题(本题15分)(1)①例题1.如图1.AB是圆O的直径,直线L与圆O有一个公共点C,过A,B分别作L的垂线,垂足为E、F,则EC=CF.第2题图BCADFE第1题图OABCNM第3题图OBCAFE第4题图ABCED②上题中,当直线L向上平行移动时,与圆O有了两个交点,其他条件不变,如图2,经过推证,我们会得到与原题相应的结论:③把直线L继续向上平行移动,使弦与AB交于点P(P不于A、B重合)在其他条件不变的情况下,请你在图3的圆中将变化后的图形画出来,标好对应的字母,并写出与①②相应的结论等式,判断你写的结论是否成立,若不成立,说明理由,若成立,给以证明。结论_____________。证明结论成立或不成立的理由附:参考答案一、选择题(本题共8小题,每小题3分,共24分)1C;2B;3B;4A;5C;6D;7C;8D.二、判断题(本题共5小题,每小题2分,共10分)1√;2×;3√;4×;5√.三、填空题(本题共4小题,每小题4分,共16分)1.45°;2.;3.60°;4.5;30°。四、计算题(8分)已知:如图,周长为40cm的等腰梯形ABCD中,AD//BC,梯形中位线EF=AB,梯形的高AH=6cm,求:梯形ABCD的面积解:提示:2EF=AD+BC2EF=AB+DC而AB+BC+CD+DA=404EF=40,得EF=10,又AH=6lͼ1OABEFClͼ2C2C1OABEFͼ3ABCED梯形ABCD的面积S=EF,AH=10×6=60(cm)2五、证明题(27分)1.已知:如右图,在等腰梯形ABCD中,AD∥BC,AB=DC,过...