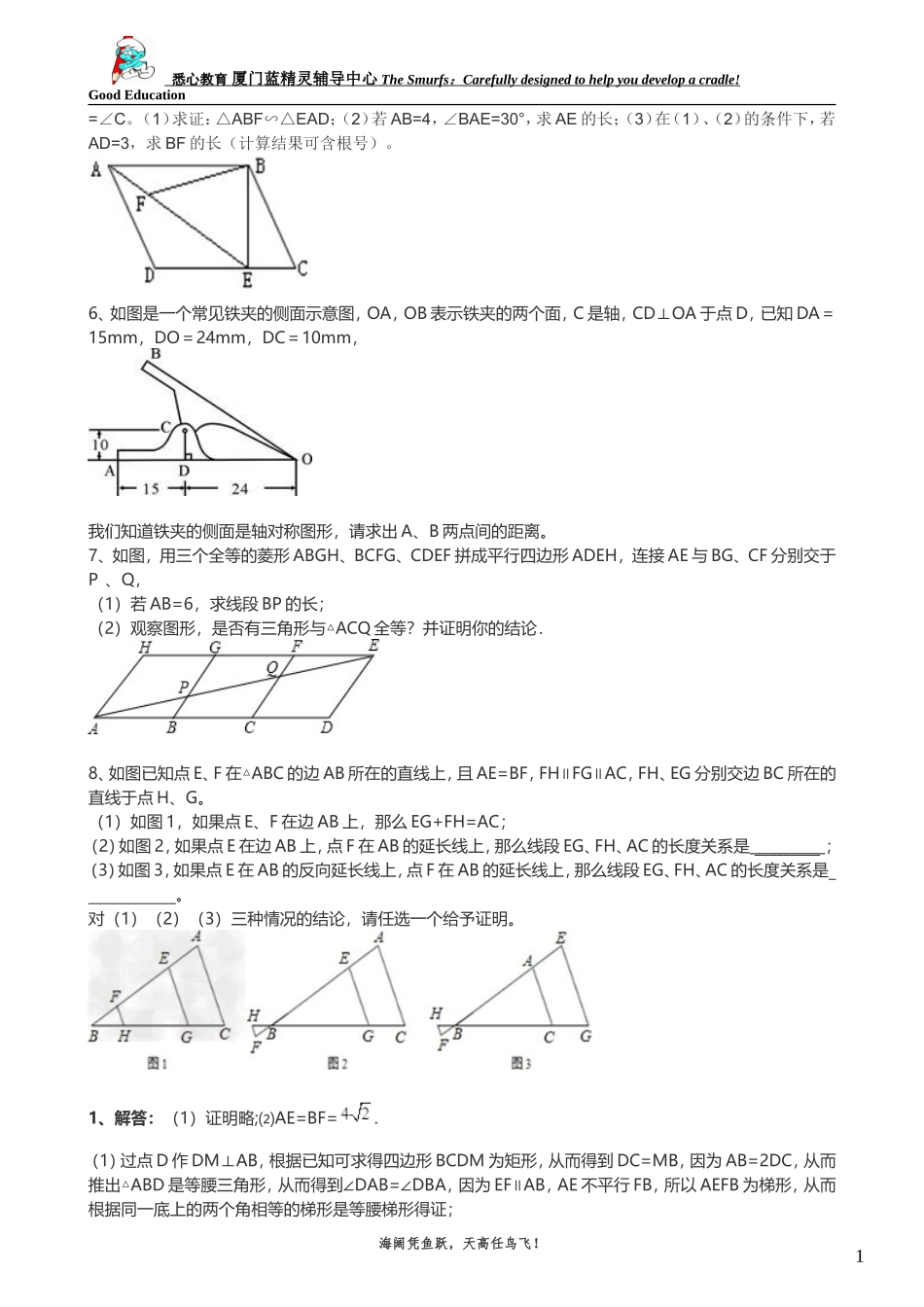
1悉心教育厦门蓝精灵辅导中心TheSmurfs:Carefullydesignedtohelpyoudevelopacradle!GoodEducation初二几何经典训练题1、如图,在直角梯形ABCD中,AB∥DC,∠ABC=90°,AB=2DC,对角线AC⊥BD,垂足为F,过点F作EF∥AB,交AD于点E,CF=4cm.⑴求证:四边形ABFE是等腰梯形;⑵求AE的长.2、如图,矩形ABCD的对角线AC、BD相交于点O,E、F分别是OA、OB的中点.(1)求证:△ADE≌△BCF;(2)若AD=4cm,AB=8cm,求CF和OF的长。3、如图,已知直角梯形ABCD中,AD∥BC,∠B=90°,AB=12cm,BC=8cm,DC=13cm,动点P沿A→D→C线路以2cm/秒的速度向C运动,动点Q沿B→C线路以1cm/秒的速度向C运动.P、Q两点分别从A、B同时出发,当其中一点到达C点时,另一点也随之停止.设运动时间为t秒,△PQB的面积为ycm2.(1)求AD的长及t的取值范围;(2)当1.5≤t≤t0(t0为(1)中t的最大值)时,求y关于t的函数关系式;(3)请具体描述:在动点P、Q的运动过程中,△PQB的面积随着t的变化而变化的规律。4、如图,AB与CD相交于E,AE=EB,CE=ED,D为线段FB的中点,GF与AB相交于点G,若CF=15cm,求GF之长。5、如图所示,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上的一点,且∠BFE海阔凭鱼跃,天高任鸟飞!1悉心教育厦门蓝精灵辅导中心TheSmurfs:Carefullydesignedtohelpyoudevelopacradle!GoodEducation=∠C。(1)求证:△ABF∽△EAD;(2)若AB=4,∠BAE=30°,求AE的长;(3)在(1)、(2)的条件下,若AD=3,求BF的长(计算结果可含根号)。6、如图是一个常见铁夹的侧面示意图,OA,OB表示铁夹的两个面,C是轴,CD⊥OA于点D,已知DA=15mm,DO=24mm,DC=10mm,我们知道铁夹的侧面是轴对称图形,请求出A、B两点间的距离。7、如图,用三个全等的菱形ABGH、BCFG、CDEF拼成平行四边形ADEH,连接AE与BG、CF分别交于P、Q,(1)若AB=6,求线段BP的长;(2)观察图形,是否有三角形与△ACQ全等?并证明你的结论.8、如图已知点E、F在△ABC的边AB所在的直线上,且AE=BF,FH∥FG∥AC,FH、EG分别交边BC所在的直线于点H、G。(1)如图1,如果点E、F在边AB上,那么EG+FH=AC;(2)如图2,如果点E在边AB上,点F在AB的延长线上,那么线段EG、FH、AC的长度关系是_________;(3)如图3,如果点E在AB的反向延长线上,点F在AB的延长线上,那么线段EG、FH、AC的长度关系是_____________。对(1)(2)(3)三种情况的结论,请任选一个给予证明。1、解答:(1)证明略;⑵AE=BF=.(1)过点D作DM⊥AB,根据已知可求得四边形BCDM为矩形,从而得到DC=MB,因为AB=2DC,从而推出△ABD是等腰三角形,从而得到∠DAB=∠DBA,因为EF∥AB,AE不平行FB,所以AEFB为梯形,从而根据同一底上的两个角相等的梯形是等腰梯形得证;海阔凭鱼跃,天高任鸟飞!1悉心教育厦门蓝精灵辅导中心TheSmurfs:Carefullydesignedtohelpyoudevelopacradle!GoodEducation(2)由已知可得到△DCF∽△BAF,根据相似三角形的对应边成比例,可得到AF的长,再根据△BCF∽△ACB,得到BF2=CF•AF,从而求得BF的长,由第一问已证得BF=AE,所以就求得了AE的长。2、解答:(1)证明: 四边形ABCD为矩形∴AD=BC,OA=OC,OB=OD,AC=BD,AD∥BC∴OA=OB=OC,∠DAE=∠OCB(两直线平行,内错角相等)∴∠OCB=∠OBC∴∠DAE=∠CBF又 AE=12OA,BF=12OB∴AE=BF∴△ADE≌△BCF;(2)过点F作FG⊥CD于点G,∴∠DGF=90° 四边形ABCD是矩形,∴∠DCB=90°∴∠DGF=∠DCB又 ∠FDG=∠BDC∴△DFG∽△DBC∴FGBC=DFDB=DGDC由(1)可知F为OB的中点,所以DF=3FB,得DFDB=34海阔凭鱼跃,天高任鸟飞!1悉心教育厦门蓝精灵辅导中心TheSmurfs:Carefullydesignedtohelpyoudevelopacradle!GoodEducation∴FG4=34=DG8∴FG=3,DG=6∴GC=DC-DG=8-6=2在Rt△FGC中,CF=FG2+GC2=9+4=13cm.(说明:其他解法可参照给分,如延长CF交AB于点H,利用△DFC∽△BFH计算.)解答:(1)略(2)∴OF=cm.(1)根据矩形的对边相等、对角线相等且相互平分等性质可证△ADE≌△BCF;(2)要求CF的长,若CF在一直角三角形中,则可用勾股定理求解.由此需要添加辅助线,过点F作FG⊥CD于点G,则△DFG∽...