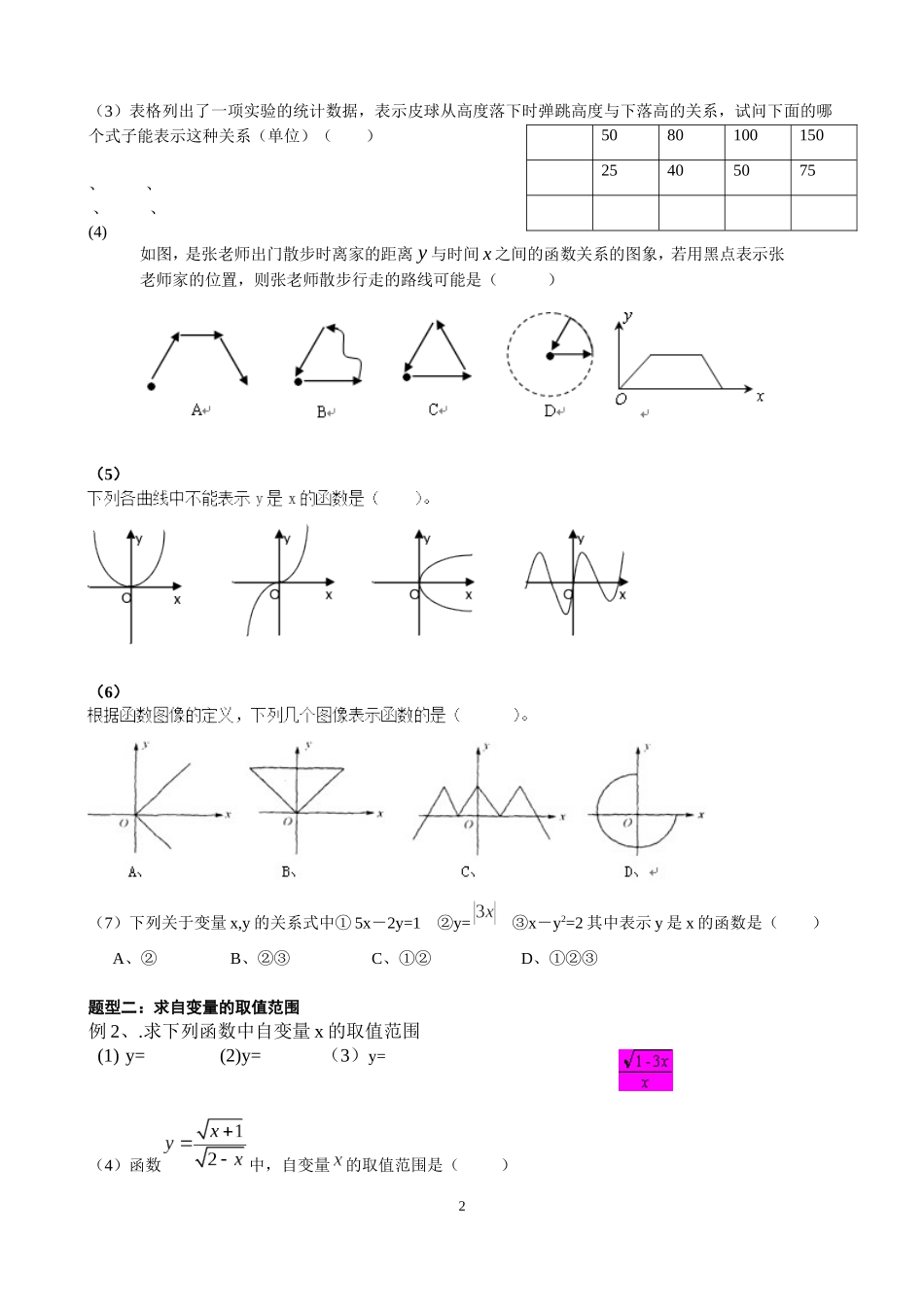
初二数学函数及图象基础知识训练第一讲函数及坐标系【知识要点】1、变量与常量在某一变化过程中,可以取不同数值的量,叫做变量,取值始终保持不变的量,称为常量2、函数的概念如果在一个变化过程中,有两个变量和,对于的每一个值,都有的唯一值与之对应,就说是自变量,是因变量,也称是的函数。3、函数关系式的表示表示函数关系的方法通常有三种:解析法、列表法、图象法。解析法是最常见的表示方法。4、平面直角坐标系的概念在平面上画两条原点重合,互相垂直且具有相同单位长度的数轴,这就建立了平面直角坐标系,其中水平的一条数轴叫做轴或者横轴,取向右为正方向;垂直的数轴叫做轴或者纵轴,取向上为正方向;两数轴的交点叫做坐标原点。5、平面直角坐标系上的点及其特征在平面直角坐标系中的点和有序实数对是一一对应的。(1)象限内点的坐标特点:(2)坐标轴上的点不属于任何象限,x轴上的点的纵坐标为0,y轴上的点的横坐标为0,原点可表示为(3)对称点的坐标特点:关于轴对称的两个点的横坐标相等(不变),纵坐标互为相反数;关于轴对称的两个点的纵坐标相等(不变),横坐标互为相反数;关于原点对称的两个点,横、纵坐标均互为相反数。6、画函数的图像画函数图象的方法可以概括为列表、描点、连线三步,通常称为三步法画函数图像。画函数图像本质上就是把函数由解析法或列表法向图像法转换的过程。函数图像上的每一个点,点的横坐标代入自变量,纵坐标代入因变量,这两个量必须满足函数解析式,或在列表中对应,反之,对应的一组自变量和因变量,作为一组有序实数对,则它所对应的点,必然在函数的图像上。题型一:函数概念及表示例1、(1)甲、乙两地相距S千米,某人行完全程所用的时间t(时)与他的速度v(千米/时)满足vt=S,在这个变化过程中,下列判断中错误的是()A.S是变量B.t是变量C.v是变量D.S是常量(2)目前,全球淡水资源日益减少,提倡全社会节约用水.据测试:拧不紧的水龙头每分钟滴出100滴水,每滴水约0.05毫升.小康同学洗手后,没有把水龙头拧紧,水龙头以测试的速度滴水,当小康离开x分钟后,水龙头滴出y毫升的水,请写出y与x之间的函数关系式是()A、y=0.05xB、y=5xC、y=100xD、y=0.05x+100(3)1(3)表格列出了一项实验的统计数据,表示皮球从高度落下时弹跳高度与下落高的关系,试问下面的哪个式子能表示这种关系(单位)()、、、、(4)(5)(6)(7)下列关于变量x,y的关系式中①5x-2y=1y=②x③-y2=2其中表示y是x的函数是()A、②B、②③C、①②D、①②③题型二:求自变量的取值范围例2、.求下列函数中自变量x的取值范围(1)y=(2)y=(3)y=(4)函数中,自变量的取值范围是()2508010015025405075如图,是张老师出门散步时离家的距离y与时间x之间的函数关系的图象,若用黑点表示张老师家的位置,则张老师散步行走的路线可能是()A、B、C、D、(5)在函数中自变量的取值范围是。(6)设一长方体盒子高20cm,底面是正方形;则这个长方体盒子的体积V(cm3)与底面边长a(cm)之间的函数关系式为,自变量的取值范围是。题型三:平面坐标系内的点的坐标例3、(1)点A的坐标满足条件,则点A的位置在:()A.第一象限B.第二象限C.第三象限D.第四象限(2)若点P()到轴的距离是2,到y轴的距离是3,则这样的点P有()A.1个B.2个C.3个D.4个(3)点在第二象限,则的取值范围是()A.B.C.D.(4)若点P(-2a-1,2a-4)关于原点对称的点在第一象限,则a的整数解有()个。A.1B.2C.3D.4(5)若点M(a+b,ab)在第二象限,则点N(a,b)在第__________象限。(6)点A(-3,4)与点B(3,4)关于___________轴对称。(7)已知点A(x,2),B(-3,y),若ABy∥轴,则x________,y___________。(8)无论x取值,点A(x+1,x-1)都不可能在第_________象限。(9)已知点M(x,y)与点N(-2,-3)关于x轴对称则x+y=__________。题型四:函数图象例4、(1)(2)3(3)(1)已知点E(1,2),F(3,),G(1,-1),H(-2,-4)。四点中在函数y=图象上的是()A、E点B、F点C、G点D、H点(4)已知点A(2,3)在函数y=ax2-x+1的图象上,则a等于(...