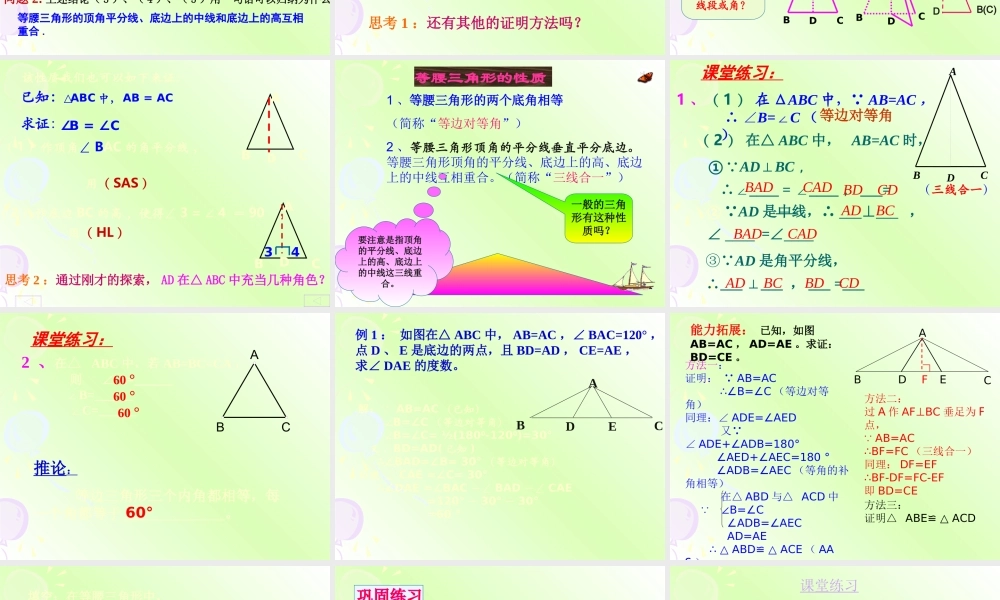
1 5.3 等腰三角形 安徽省临泉四中 常文玉 下载图片 等腰三角形一 . 基本概念 1. 定义 :两条边相等的三角形叫做等腰三角形 . 如图 AB=AC , 就是等腰三角形 ABC2. 等腰三角形的基本要素 :ABC腰腰底边顶角底角底角( 1 )、等腰三角形是轴对称图形( 2 )、∠ B =∠ C,( 3 )、 BD = CD,( 4 )、∠ ADB = ∠ADC = 90°,( 5 )、∠ BAD = ∠CAD ,CABD问题 1: 上述结论( 2 )用文字如何表述?等腰三角形的两个底角相等 .问题 2: 上述结论( 3 )、( 4 )、( 5 )用一句话可以归纳为什么?等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合 .即两底角相等即 AD 为底边上的中线即 AD 为底边上的高即 AD 为顶角平分线CABD如何证明:等腰三角形的两个底角相等?已知:如图△ ABC 中 AB=AC求证:∠ B=C∠证明:作 BC 上的中线 AD 在△ ABD 和△ ACD 中 ∴△ ABD ≌ △ACD(SSS) ∴∠B=∠C思考 1 :还有其他的证明方法吗?BDCDABACADAD做一做 1 : ( 1 )把准备的等腰三角形纸片拿出来;( 2 )把三角形的顶角顶点记为 A ,底角顶点记为 B , C 。( 3 )把三角形对折,让两腰 AB , AC 重叠在一起,折痕为 AD 。 二 . 等腰三角形性质的探索BACDABCDAB(C)D 通过折叠你发现图形中有哪些相等的线段或角?已知:求证:△ABC 中, AB = AC∠B = ∠CABCABC( 1 )作顶角∠ BAC 的角平分线 ,D34( 2 )作底边 BC 的高 ,使得∠ 3 = ∠ 4 = 90 ,。用( SAS )用( HL )该性质我们也可以如下来证:思考 2 :通过刚才的探索, AD 在△ ABC 中充当几种角色?D等腰三角形的性质1 、等腰三角形的两个底角相等(简称“等边对等角”)2 、等腰三角形顶角的平分线垂直平分底边。等腰三角形顶角的平分线、底边上的高、底边上的中线互相重合。(简称“三线合一”)一般的三角形有这种性质吗?要注意是指顶角的平分线、底边上的高、底边上的中线这三线重合。CDBA1 、( 1 ) 在 ΔABC 中, AB=AC , ∴ ∠B=∠C ( )等边对等角① AD⊥BC ,∴∠____ = ____∠, ___= ___ ② AD 是中线,∴ ___⊥___ ,∠ ____ =∠____③ AD 是角平分线,∴___ ___ ⊥, ___ =___BAD CAD BD CD AD BC AD BCBAD CADBD CD( 2 ) 在△ ABC 中, AB...