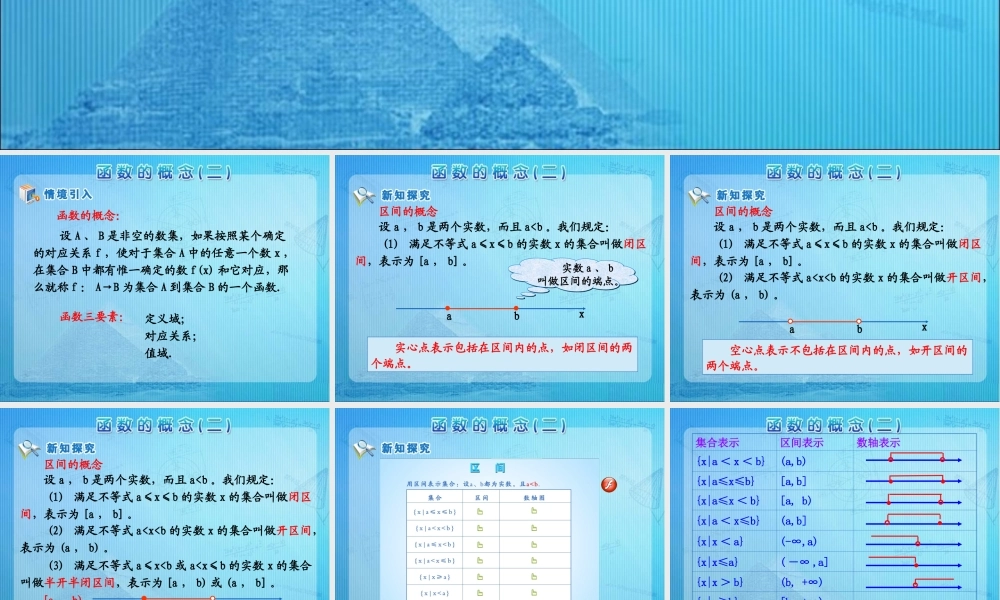
函数的概念:函数三要素: 设 A 、 B 是非空的数集,如果按照某个确定的对应关系 f ,使对于集合 A 中的任意一个数 x ,在集合 B 中都有惟一确定的数 f(x) 和它对应,那么就称 f : A→B 为集合 A 到集合 B 的一个函数.定义域;对应关系;值域.区间的概念 设 a , b 是两个实数,而且 a0 时,求 f(a) , f(a-1) 的值。23分析: 函数的定义域通常是由问题的实际背景确定的。如果只给出解析式 y=f(x) ,而没有指明它的定义域,那么函数的定义域就是指能使这个式子有意义的实数的集合。 研究一个函数一定在其定义域内研究,所以求定义域是研究任何函数的前提。解: 使根式 有意义的实数 x 的集合为 {x|x≥-3} 。x+3 使分式 有意义的实数 x 的集合为 {x|x≠-2} 。1x+2要使函数有意义,需同时使得根式、分式都有意义。( 1)例 1 已知函数 f(x)= x+3 + ,1x+2(1) 求函数的定义域;(2) 求 f(-3) , f( ) 的值;(3) 当 a>0 时,求 f(a) , f(a-1...