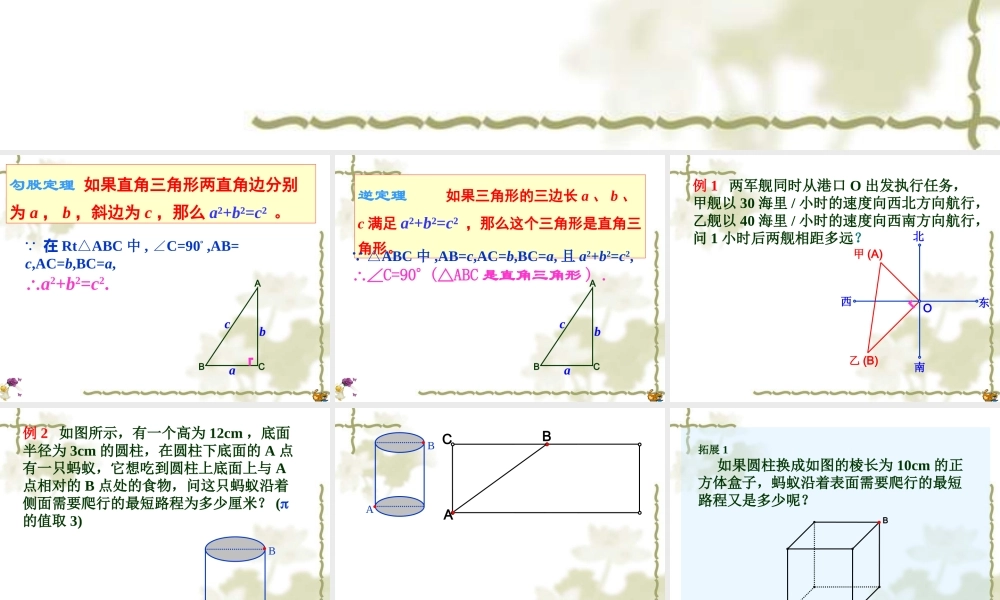
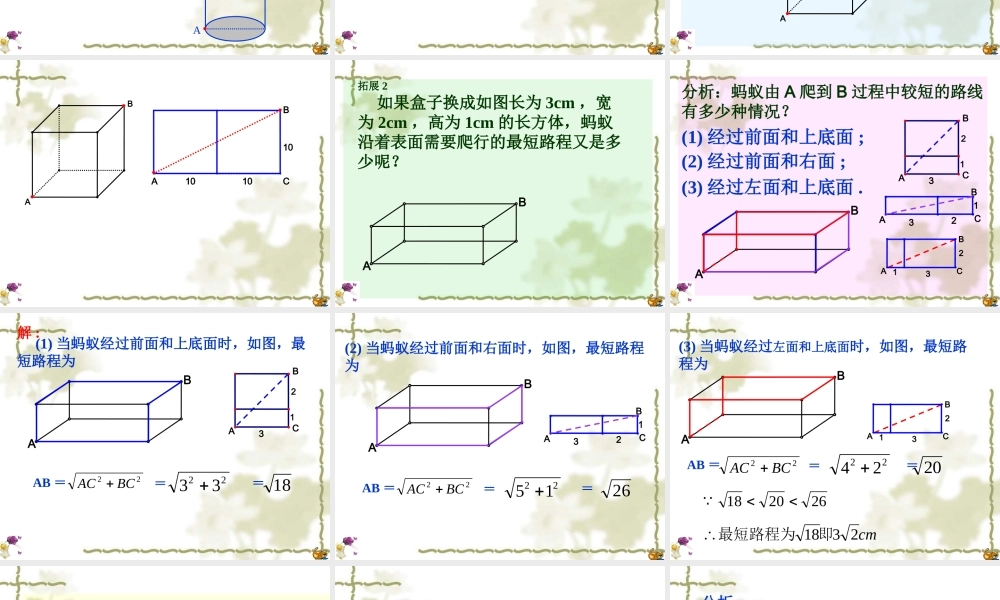
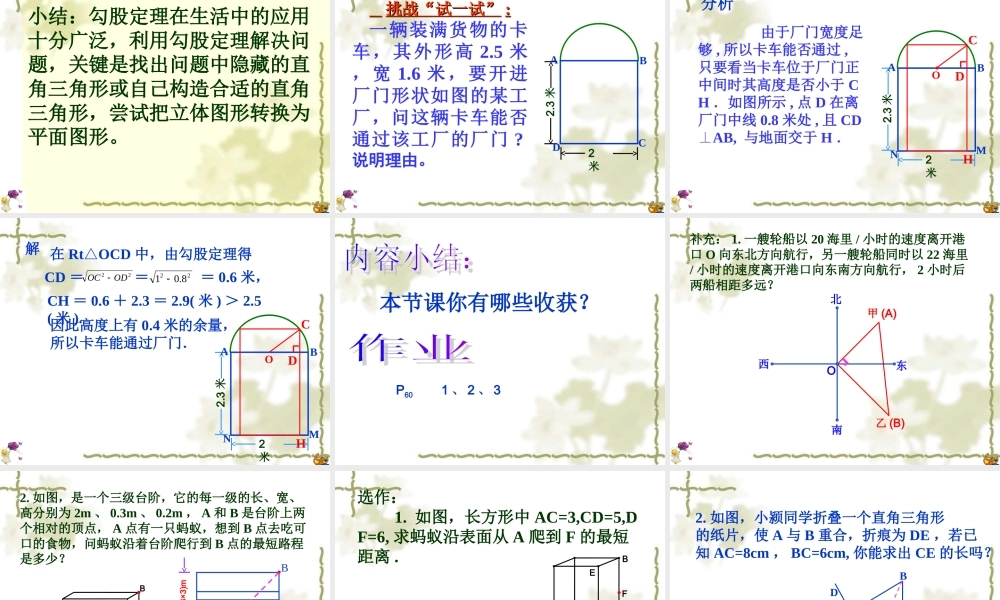
勾股定理 如果直角三角形两直角边分别为 a , b ,斜边为 c ,那么 a²+b²=c² 。cabABC 在 RtABC△中 , C=90∠º ,AB=c,AC=b,BC=a,a2+b2=c2.┏ 逆定理 如果三角形的三边长 a 、 b 、c 满足 a²+b²=c² ,那么这个三角形是直角三角形。 △ABC 中 ,AB=c,AC=b,BC=a, 且 a2+b2=c2,∠C=90º (△ABC 是直角三角形 ) .cabABC 例 1 两军舰同时从港口 O 出发执行任务,甲舰以 30 海里 / 小时的速度向西北方向航行,乙舰以 40 海里 / 小时的速度向西南方向航行,问 1 小时后两舰相距多远?甲 (A)西东北南O乙 (B)┏ AB例 2 如图所示,有一个高为 12cm ,底面半径为 3cm 的圆柱,在圆柱下底面的 A 点有一只蚂蚁,它想吃到圆柱上底面上与 A点相对的 B 点处的食物,问这只蚂蚁沿着侧面需要爬行的最短路程为多少厘米? (的值取 3) ACBAB 拓展 1 如果圆柱换成如图的棱长为 10cm 的正方体盒子,蚂蚁沿着表面需要爬行的最短路程又是多少呢?AB AB101010BCA 拓展 2 如果盒子换成如图长为 3cm ,宽为 2cm ,高为 1cm 的长方体,蚂蚁沿着表面需要爬行的最短路程又是多少呢?AB 分析:蚂蚁由 A 爬到 B 过程中较短的路线有多少种情况?(1) 经过前面和上底面 ;(2) 经过前面和右面 ;(3) 经过左面和上底面 .AB23AB1C321BCA321BCA (1) 当蚂蚁经过前面和上底面时,如图,最短路程为2233 18解 :AB23AB1C22BCAC AB === (2) 当蚂蚁经过前面和右面时,如图,最短路程为22BCAC 2215 26AB321BCAAB === (3) 当蚂蚁经过左面和上底面时,如图,最短路程为AB22BCAC 2224 20262018cm2318即最短路程为AB ===321BCA 小结:勾股定理在生活中的应用十分广泛,利用勾股定理解决问题,关键是找出问题中隐藏的直角三角形或自己构造合适的直角三角形,尝试把立体图形转换为平面图形。 挑战“试一试”挑战“试一试” ::一辆装满货物的卡车,其外形高 2.5 米,宽 1.6 米,要开进厂门形状如图的某工厂,问这辆卡车能否通过该工厂的厂门 ?说明理由。 ABCD2米2.3 米 ABMNOC┏D分析H2米2.3 米 由于厂门宽度足够 , 所以卡车能否通过 ,只要看当卡车位于厂门正中间时其高度是否小于 CH .如图所示 , 点 D 在离厂门中线 0.8 米处 , 且 CDAB, ⊥与地面交于 H . 解CD =22ODOC 228.01 CH = 0.6 + 2.3 ...