圆周角PPTVIP免费

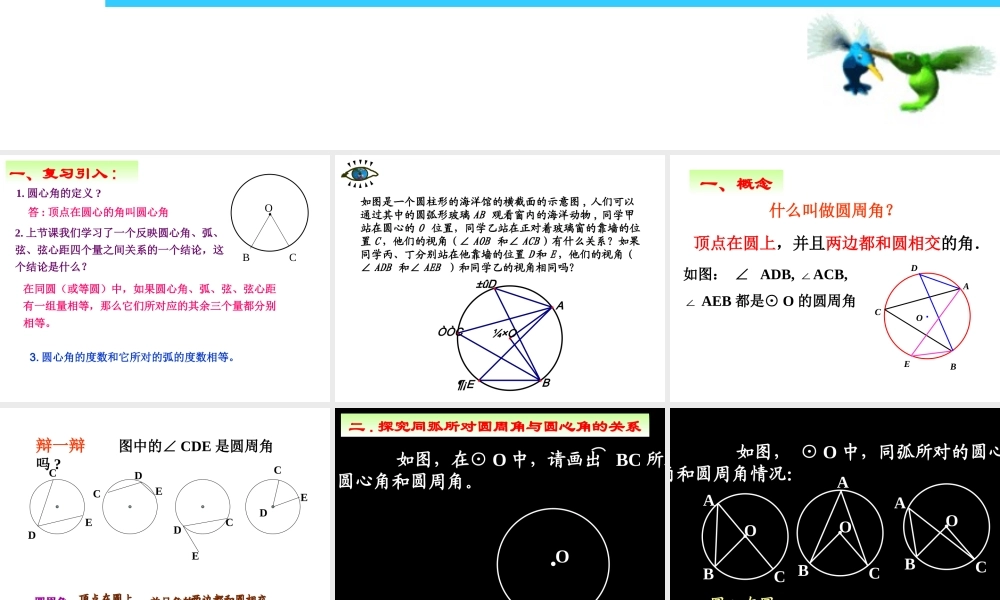
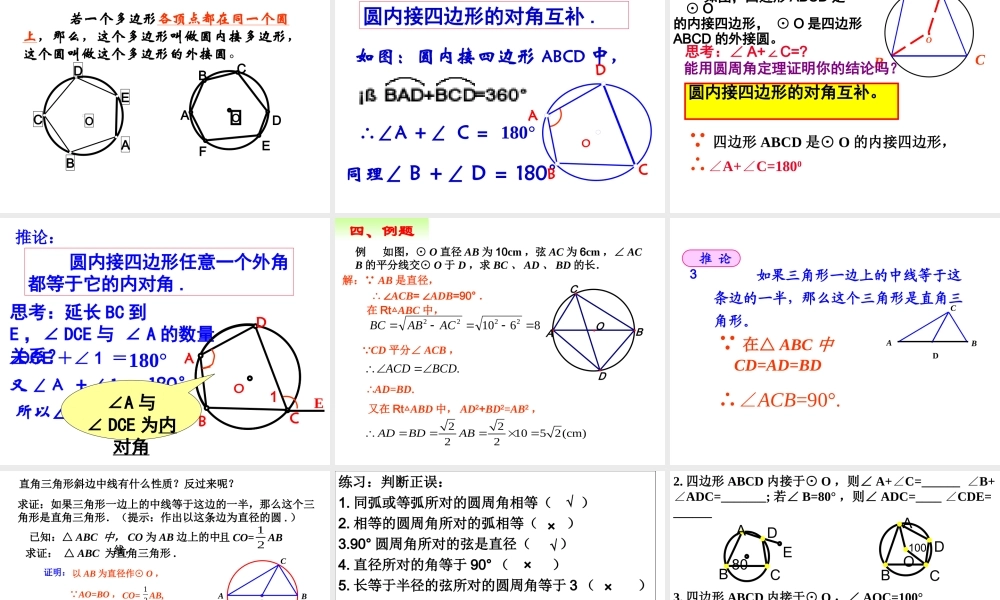
1. 圆心角的定义 ?.OBC在同圆（或等圆）中，如果圆心角、弧、弦、弦心距有一组量相等，那么它们所对应的其余三个量都分别相等。答 : 顶点在圆心的角叫圆心角2. 上节课我们学习了一个反映圆心角、弧、弦、弦心距四个量之间关系的一个结论，这个结论是什么？一、复习引入 :3. 圆心角的度数和它所对的弧的度数相等。如图是一个圆柱形的海洋馆的横截面的示意图 , 人们可以通过其中的圆弧形玻璃 AB 观看窗内的海洋动物 , 同学甲站在圆心的 O 位置，同学乙站在正对着玻璃窗的靠墙的位置 C ，他们的视角（∠ AOB 和∠ ACB ）有什么关系？如果同学丙、丁分别站在他靠墙的位置 D 和 E ，他们的视角（ ∠ ADB 和∠ AEB ）和同学乙的视角相同吗？¼×OBA±ûDÒÒC¶¡E 顶点在圆上，并且两边都和圆相交的角．什么叫做圆周角？·ABCDEO一、概念如图： ∠ ADB, ACB, ∠ ∠ AEB 都是⊙ O 的圆周角辩一辩 图中的∠ CDE 是圆周角吗 ?CDECDECDECDE圆周角：圆周角： ____________________ ，并且角的，并且角的 ____________________________ 。。圆心角圆心角 :: ___________ ___________ 的角的角 ..顶点在圆上顶点在圆上两边都和圆相交两边都和圆相交顶点在圆心顶点在圆心 如图，在⊙ O 中，请画出 BC 所对的圆心角和圆周角。CBO二 . 探究同弧所对圆周角与圆心角的关系 如图， ⊙ O 中，同弧所对的圆心角和圆周角情况：CBOACBOACBOA 圆心在圆周角内部 圆心在圆周角一边上 圆心在圆周角外部（ 1 ）在圆周角的一条边上；·COABBOCA21即 OA=OC ，∴∠A=∠C ．又∠ BOC=∠A+∠C∴∠BOC=2∠A（ 2 ）在圆周角的内部．CB·OD圆心 O 在∠ BAC 的内部，作直径 AD ，利用（１）的结果，有12DACDOC 1 ()2BADDACBODDOC12BACBOC A（ 3 ）在圆周角的外部．12BADBOD 12DACDOC 1 ()2DACDABDOCDOB  12BACBOC 圆心 O 在∠ BAC 的外部，作直径 AD ，利用（１）的结果，有·COABD结论：一条弧所对的圆周角等于它所对的圆心角的一半． 归纳 在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对圆心角的一半。圆周角定理：CBOACBOACBOA: A = 1/2BOC∠∠或 ∠BOC=2A∠ 21 OCAB1 、已知∠ AOB ＝ 75° ， 求：∠ ACB= OCAB 2 、已知∠ AOB ＝ 120° ， 求： ∠ ACB...