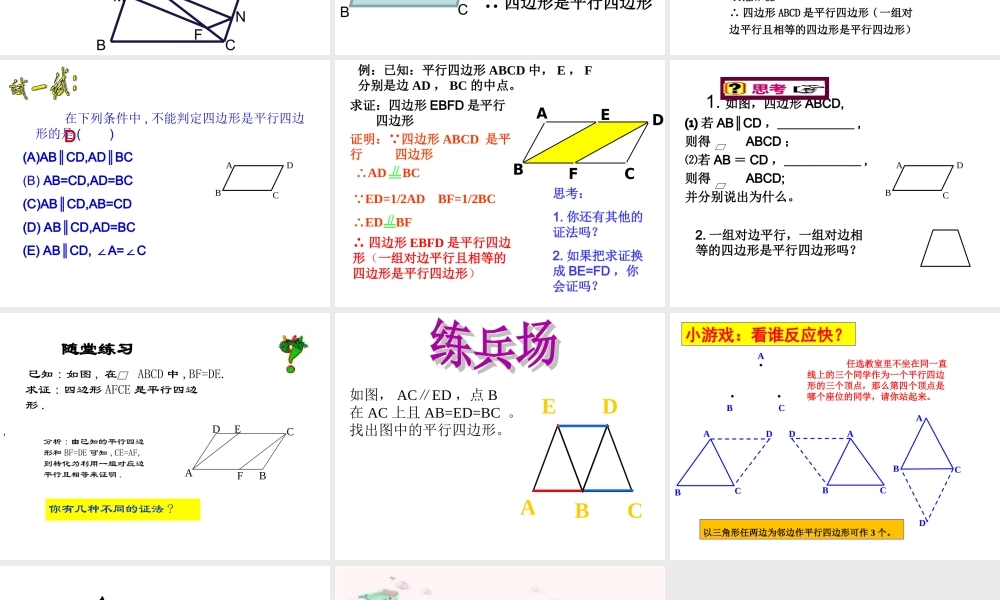
平行四边形的性质:边平行四边形的对边平行平行四边形的对边相等角平行四边形的对角相等平行四边形的邻角互补对角线 平行四边形的对角线 互相平分ABCD求证:四边形 ABCD 是平行四边形。 证明:连接 AC . AD∥BC ∴∠DAC=∠ACB AD=CB , AC=CA , ∴ΔADC≌ΔCBA ( S.A.S.)∴∠ACD=∠CAB∴AB∥CD ∴ 四边形 ABCD 是平行四边形 (平行四边形的定义)已知:在四边形 ABCD 中, AD BC 。两组对边分别平行的四边形是平行四边形。BDACO已知:四边形 ABCD, AC 、 BD 交于点 O 且 OA=OC , OB=OD求证:四边形 ABCD 是平行四边形4213证明: AO = CO , BO = DO ,∠ 1 = ∠2∴△AOB≌△COD∴AB ∥ CD 同理 AD ∥ BC∴ 四边形 ABCD 是平行四边形(两组对边分别平行的四边形是平行四边形)∴ ∠3 = ∠4判定二两组对边分别相等的四边形是平行四边形• 在平行四边形 ABCD 中, M,N 分别是 AB, CD 上的点, AM=CN,E,F 是 AC 上的点且 AE=CF. 求证:四边形 MENF 是平行四边形DBANEFMC 一组对边平行且相等的四边形是平行四边形ADCB几何语言 : AB∥CD , AB = CD∴ 四边形是平行四边形求证:四边形 ABCD 是平行四边形。 证明:连接 AC . AD=CB , AC=CA , CD=AB, ∴ΔADC≌ΔCBA ( S.S.S.)∴∠ACD=∠CAB∴AB∥CD ∴ 四边形 ABCD 是平行四边形 ( 一组对边平行且相等的四边形是平行四边形) 已知 : 在四边形 ABCD 中 , AD=BC,AB=CD.一组对边平行且相等的四边形是平行四边形)。BACD在 ΔADC 和 ΔCBA 中, 在下列条件中 , 不能判定四边形是平行四边形的是 ( )(A)AB CD,AD BC∥∥ (B) AB=CD,AD=BC (C)AB CD,AB=CD ∥(D) AB CD,AD=BC∥(E) AB CD, A=C∥∠∠DABCD例:已知:平行四边形 ABCD 中, E , F分别是边 AD , BC 的中点。 求证:四边形 EBFD 是平行 四边形证明: 四边形 ABCD 是平行 四边形 ∴AD BC ED=1/2AD BF=1/2BC ∴ED BF ∴ 四边形 EBFD 是平行四边形(一组对边平行且相等的四边形是平行四边形)ABCDEF思考:1. 你还有其他的证法吗?2. 如果把求证换成 BE=FD ,你会证吗? 1. 如图,四边形 ABCD,⑴ 若 AB CD∥,______ ,则得 ABCD ;⑵若 AB = CD ,______ ,则得 ABCD; 并分别说出为什么。 ABCD思考思考思考思考2. 一组对边平行,一组对...