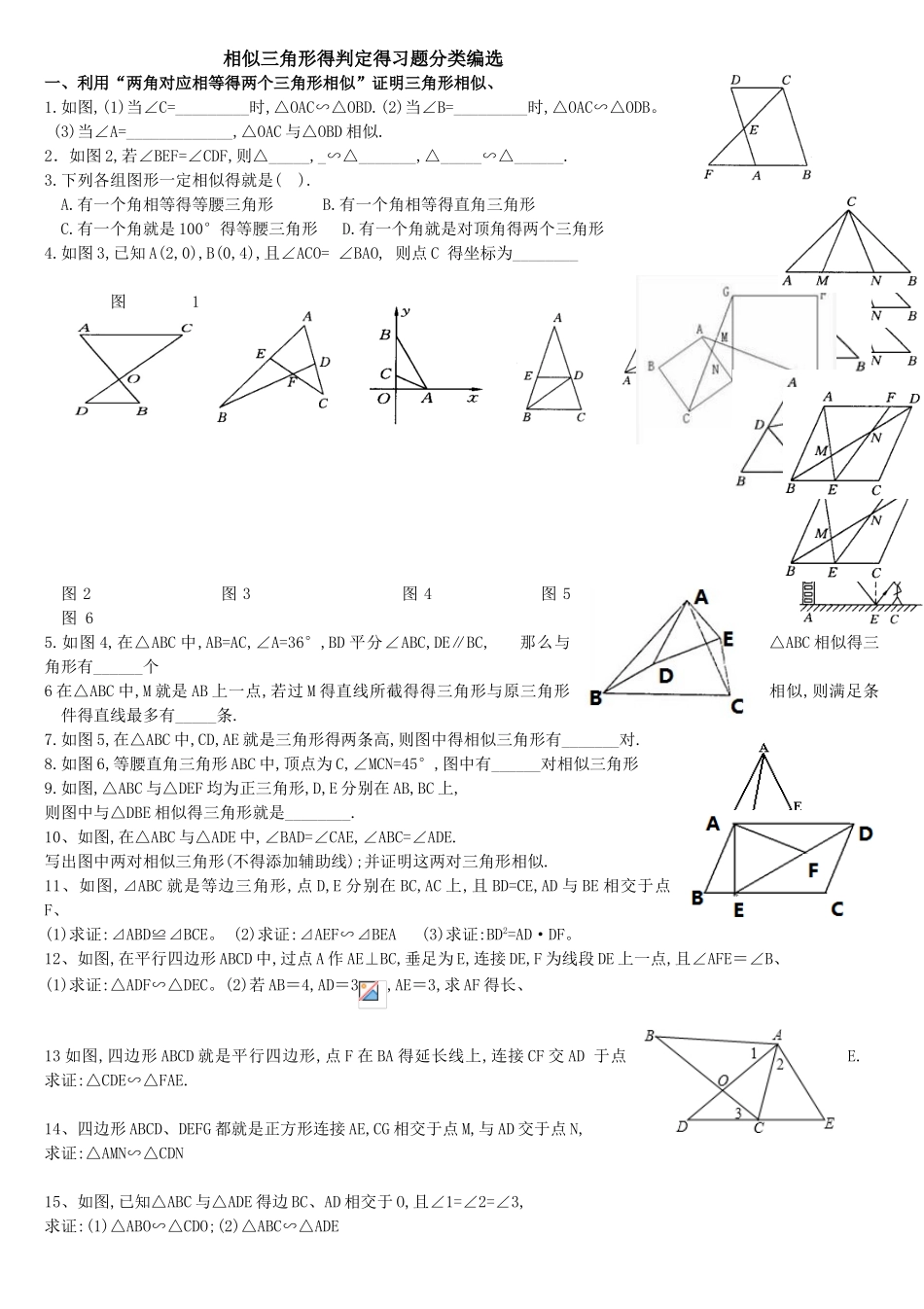
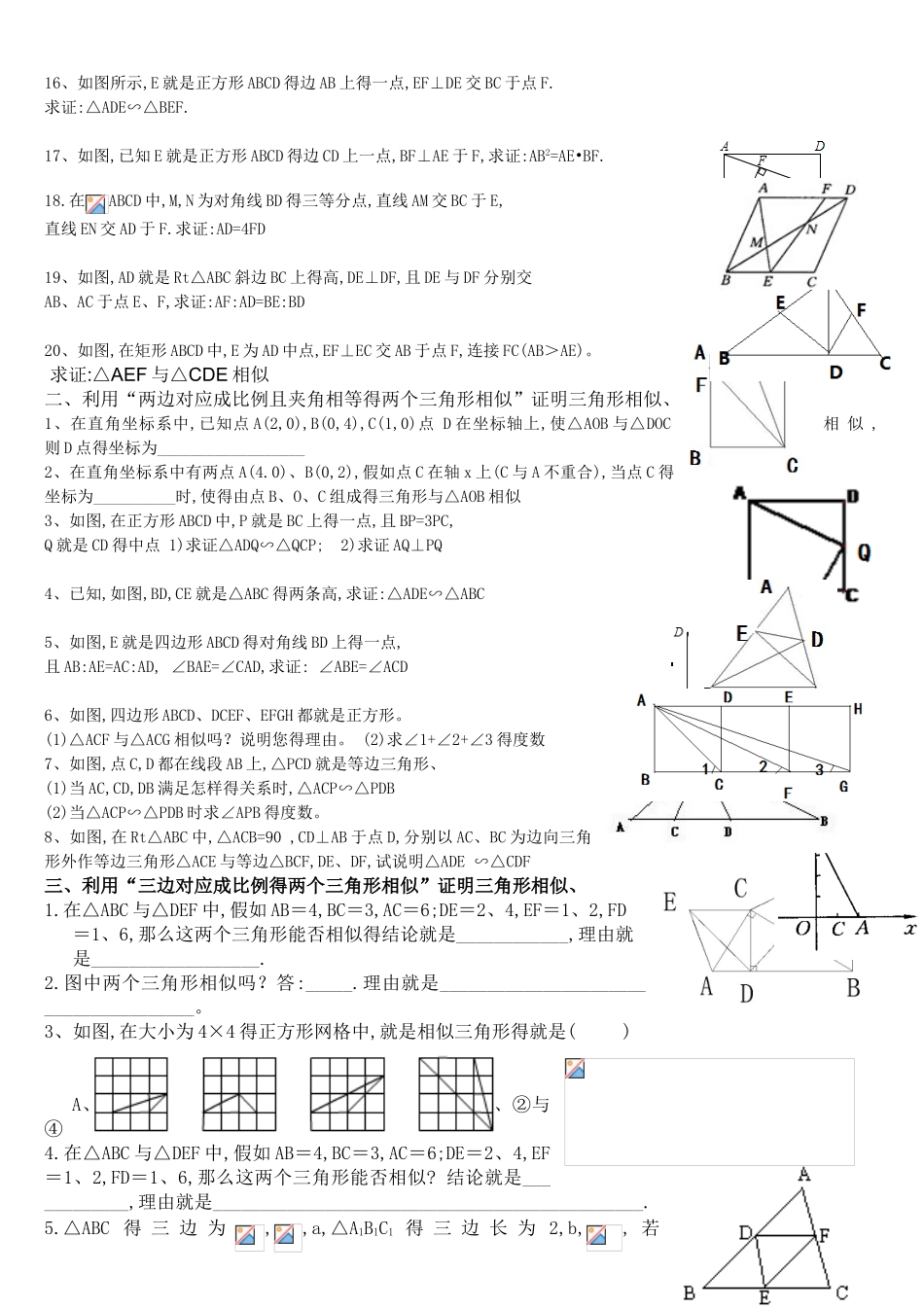
相似三角形得判定得习题分类编选一、利用“两角对应相等得两个三角形相似”证明三角形相似、1.如图,(1)当∠C=_________时,△OAC∽△OBD.(2)当∠B=_________时,△OAC∽△ODB。 (3)当∠A=_____________,△OAC 与△OBD 相似.2.如图 2,若∠BEF=∠CDF,则△_____,_∽△_______,△_____∽△______. 3.下列各组图形一定相似得就是( ). A.有一个角相等得等腰三角形 B.有一个角相等得直角三角形 C.有一个角就是 100°得等腰三角形 D.有一个角就是对顶角得两个三角形 4.如图 3,已知 A(2,0),B(0,4),且∠ACO=∠BAO,则点 C得坐标为________图1 图 2 图 3 图 4 图 5 图 65.如图 4,在△ABC 中,AB=AC,∠A=36°,BD 平分∠ABC,DE∥BC, 那么与△ABC 相似得三角形有______个6 在△ABC 中,M 就是 AB 上一点,若过 M 得直线所截得得三角形与原三角形相似,则满足条件得直线最多有_____条.7.如图 5,在△ABC 中,CD,AE 就是三角形得两条高,则图中得相似三角形有_______对.8.如图 6,等腰直角三角形 ABC 中,顶点为 C,∠MCN=45°,图中有______对相似三角形9.如图,△ABC 与△DEF 均为正三角形,D,E 分别在 AB,BC 上,则图中与△DBE 相似得三角形就是________.10、如图,在△ABC 与△ADE 中,∠BAD=∠CAE,∠ABC=∠ADE.写出图中两对相似三角形(不得添加辅助线);并证明这两对三角形相似.11、如图,⊿ABC 就是等边三角形,点 D,E 分别在 BC,AC 上,且 BD=CE,AD 与 BE 相交于点F、(1)求证:⊿ABD≌⊿BCE。 (2)求证:⊿AEF∽⊿BEA (3)求证:BD2=AD·DF。12、如图,在平行四边形 ABCD 中,过点 A 作 AE⊥BC,垂足为 E,连接 DE,F 为线段 DE 上一点,且∠AFE=∠B、(1)求证:△ADF∽△DEC。(2)若 AB=4,AD=3,AE=3,求 AF 得长、13 如图,四边形 ABCD 就是平行四边形,点 F 在 BA 得延长线上,连接 CF 交 AD于点E.求证:△CDE∽△FAE.14、四边形 ABCD、DEFG 都就是正方形连接 AE,CG 相交于点 M,与 AD 交于点 N,求证:△AMN∽△CDN15、如图,已知△ABC 与△ADE 得边 BC、AD 相交于 O,且∠1=∠2=∠3,求证:(1)△ABO∽△CDO;(2)△ABC∽△ADE16、如图所示,E 就是正方形 ABCD 得边 AB 上得一点,EF⊥DE 交 BC 于点 F.求证:△ADE∽△BEF.17、如图,已知 E 就是正方形 ABCD 得边 CD 上一点,BF⊥AE 于 F,求证:AB2=AE•BF.18.在ABCD 中,M,N 为对角线 BD 得三等分点,直线 AM 交 BC 于 E,直线 ...