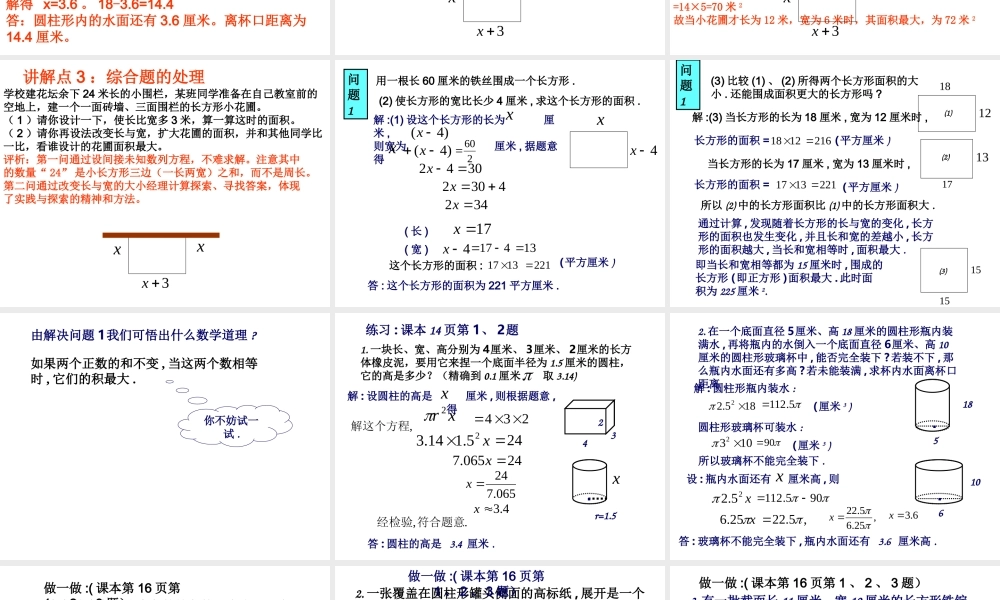
6.3 实践与探索 (1)图形的有关计算讲解点 1 :列方程解应用题的一般步骤审、设、列、解、验、答例 1 :某仓库存放的面粉运出 15% 后,还剩下 42500 千克,这个仓库原来有多少千克面粉?解:设这个仓库原来有 x 千克面粉,根据题意,得 x-15%x=42500解得 x=50000答:这个仓库原来有 50000 千克面粉。评析:本题隐含的相等关系是: 原来重量 - 运出重量 = 剩余重量讲解点 2 :关于面积、周长、体积等问题中的数量关系关于图形方面的实际问题大多涉及图形的面积、周长和体积等数量关系。要解决这类问题,应从有关图形的面积、周长、体积等计算公式出发,根据题目中这些量的变化,建立相等关系,从而列出方程。有关公式如下:( 1 )长方形的周长、面积公式C 长方形 =2( 长 + 宽 ) ,s 长方形 = 长 × 宽( 2 )长方体、圆柱的体积公式V 长方体 = 长 × 宽 × 高,V 圆柱 =∏r2h例 2 :在一个底面直径 5 厘米、高 18 厘米的圆柱形瓶内装满水,再将瓶内的水倒入一个底面直径 6厘米、高 10 厘米的圆柱形玻璃杯中,能否完全装下?若装不下,那么瓶内的水面还有多高?若未能装满,求杯内水面离杯口的距离?解:( 1 )圆柱形瓶内的水为∏ ×2.52×18 =225/2∏ 圆柱形玻璃杯的容积为∏ ×32×10=90∏ 因为 225/2∏>90∏ ,所以不能完全装下。( 2 )设圆柱形瓶内的水面还有 x 厘米。根据题意,得∏ ×2.52×x=225/2∏-90∏ 解得 x=3.6 。 18-3.6=14.4答:圆柱形内的水面还有 3.6 厘米。离杯口距离为14.4 厘米。学校建花坛余下 24 米长的小围栏,某班同学准备在自己教室前的空地上,建一个一面砖墙、三面围栏的长方形小花圃。( 1 )请你设计一下,使长比宽多 3 米,算一算这时的面积。( 2 )请你再设法改变长与宽,扩大花圃的面积,并和其他同学比一比,看谁设计的花圃面积最大。x解 :(1) 设这个长方形小花圃的宽为 x 米,则长为( x+3 )米, 根据题意,得( x+3 ) +2x=24 解得 x=7 , x+3=10 这时长方形小花圃的面积为 10×7=70 米 2讲解点 3 :综合题的处理x3x学校建花坛余下 24 米长的小围栏,某班同学准备在自己教室前的空地上,建一个一面砖墙、三面围栏的长方形小花圃。( 1 )请你设计一下,使长比宽多 3 米,算一算这时的面积。( 2 )请你再设法改变长与宽,扩大花圃的面积,并和其他同学比一比,看谁设计的花圃面积最大...